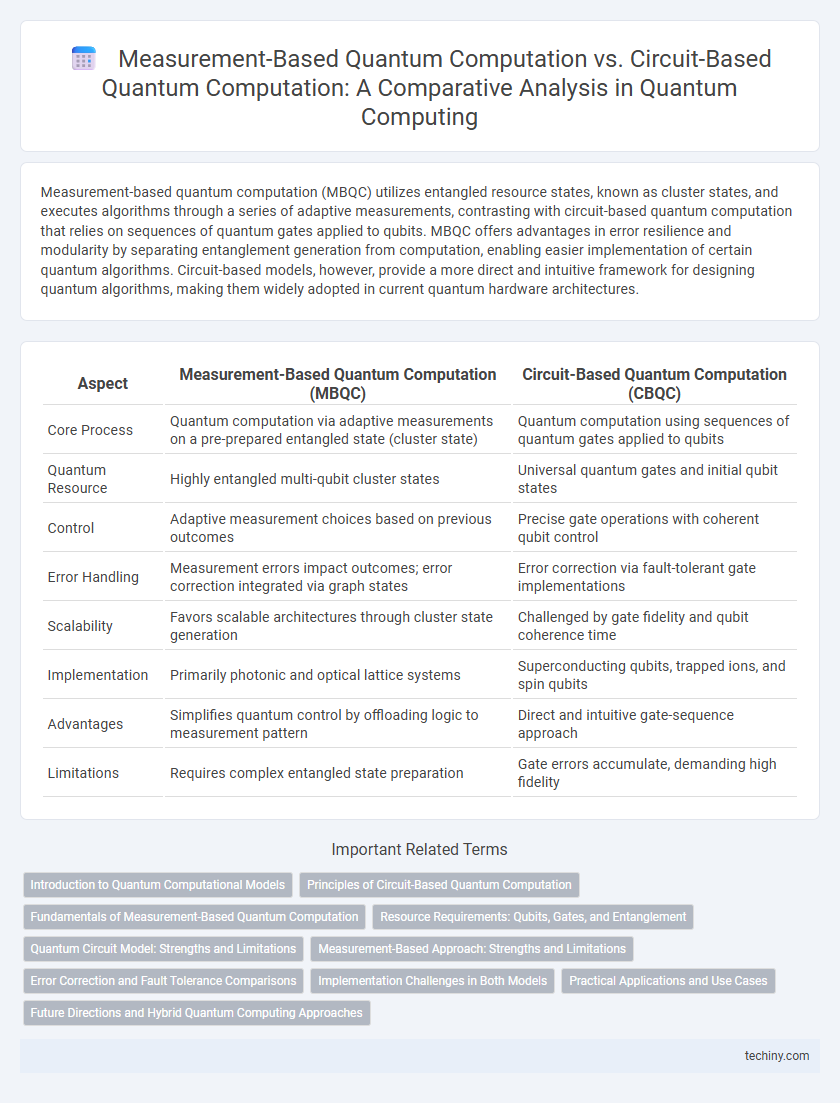
Measurement-based quantum computation (MBQC) utilizes entangled resource states, known as cluster states, and executes algorithms through a series of adaptive measurements, contrasting with circuit-based quantum computation that relies on sequences of quantum gates applied to qubits. MBQC offers advantages in error resilience and modularity by separating entanglement generation from computation, enabling easier implementation of certain quantum algorithms. Circuit-based models, however, provide a more direct and intuitive framework for designing quantum algorithms, making them widely adopted in current quantum hardware architectures.
Table of Comparison
| Aspect | Measurement-Based Quantum Computation (MBQC) | Circuit-Based Quantum Computation (CBQC) |
|---|---|---|
| Core Process | Quantum computation via adaptive measurements on a pre-prepared entangled state (cluster state) | Quantum computation using sequences of quantum gates applied to qubits |
| Quantum Resource | Highly entangled multi-qubit cluster states | Universal quantum gates and initial qubit states |
| Control | Adaptive measurement choices based on previous outcomes | Precise gate operations with coherent qubit control |
| Error Handling | Measurement errors impact outcomes; error correction integrated via graph states | Error correction via fault-tolerant gate implementations |
| Scalability | Favors scalable architectures through cluster state generation | Challenged by gate fidelity and qubit coherence time |
| Implementation | Primarily photonic and optical lattice systems | Superconducting qubits, trapped ions, and spin qubits |
| Advantages | Simplifies quantum control by offloading logic to measurement pattern | Direct and intuitive gate-sequence approach |
| Limitations | Requires complex entangled state preparation | Gate errors accumulate, demanding high fidelity |
Introduction to Quantum Computational Models
Measurement-based quantum computation relies on entangled resource states, such as cluster states, to perform quantum algorithms through adaptive single-qubit measurements, contrasting with circuit-based quantum computation that applies sequences of unitary gates directly to qubits. Circuit-based models emphasize gate fidelity and coherence time, while measurement-based models focus on entanglement depth and measurement adaptivity to achieve universal quantum computation. Both paradigms contribute to understanding quantum computational complexity and error correction strategies in quantum information processing.
Principles of Circuit-Based Quantum Computation
Circuit-based quantum computation operates on qubits using a sequence of quantum gates arranged in a circuit to perform algorithms. Each gate represents a unitary operation controlling the state transformations of qubits, enabling complex quantum state manipulations through precise control of superposition and entanglement. Quantum circuits rely on coherence and error correction techniques to maintain fidelity throughout the computation process.
Fundamentals of Measurement-Based Quantum Computation
Measurement-based quantum computation (MBQC) relies on preparing a highly entangled resource state, such as a cluster state, followed by adaptive single-qubit measurements to drive the computation. Unlike circuit-based quantum computation, which uses a sequence of quantum gates acting on qubits, MBQC encodes the algorithm in the pattern of measurements and their bases, making measurements the core operational mechanism. The computational power derives from the entanglement structure and the classical feedforward of measurement outcomes, highlighting the fundamental shift from unitary gate evolution to measurement-driven processes.
Resource Requirements: Qubits, Gates, and Entanglement
Measurement-based quantum computation requires a highly entangled resource state, such as a cluster state, consuming a large number of qubits upfront but reducing the need for dynamic gate operations during computation. Circuit-based quantum computation demands sequential application of quantum gates on qubits, often leading to increased gate depth and coherence time requirements. The entanglement in measurement-based schemes is pre-established and static, while circuit-based approaches generate entanglement dynamically through gate interactions, influencing resource allocation for qubits and gate fidelity.
Quantum Circuit Model: Strengths and Limitations
The Quantum Circuit Model offers a structured approach to quantum computation using sequences of quantum gates applied to qubits, providing clear frameworks for algorithm design and error correction techniques vital in quantum error mitigation. Its strengths lie in the modularity of gate operations and compatibility with existing quantum hardware architectures, enabling scalable quantum algorithms such as Shor's and Grover's algorithms. However, limitations include susceptibility to cumulative gate errors and challenges in implementing long-depth circuits on current noisy intermediate-scale quantum (NISQ) devices, constraining practical computation depth and fidelity.
Measurement-Based Approach: Strengths and Limitations
Measurement-based quantum computation (MBQC) leverages highly entangled resource states, known as cluster states, enabling computations through adaptive single-qubit measurements that simplify hardware requirements compared to circuit-based architectures. Its strengths include robustness to certain errors and the potential for more straightforward parallelization in quantum algorithms, while limitations involve the complexity of preparing large-scale, high-fidelity entangled states and the overhead of adaptive measurement protocols. This approach contrasts with circuit-based models by emphasizing a fundamentally different paradigm that reduces gate complexity but requires precise control in measurement timing and feedback.
Error Correction and Fault Tolerance Comparisons
Measurement-based quantum computation (MBQC) leverages cluster states to perform computations through adaptive single-qubit measurements, offering intrinsic error resilience due to its entanglement structure, which can simplify fault-tolerant protocols. In contrast, circuit-based quantum computation relies heavily on quantum gate operations that necessitate complex error correction codes like surface codes to mitigate gate errors and decoherence effects. MBQC's error correction often integrates naturally with its measurement patterns, whereas circuit-based approaches depend on active error detection and correction cycles, impacting scalability and fault tolerance thresholds differently.
Implementation Challenges in Both Models
Measurement-based quantum computation faces implementation challenges such as the need for large-scale entangled resource states like cluster states, which are difficult to generate and maintain with high fidelity. Circuit-based quantum computation struggles with error rates due to gate imperfections and requires precise qubit control and coherence preservation throughout complex sequences of quantum gates. Both models demand advances in qubit scalability, error correction techniques, and noise reduction to realize practical quantum computing systems.
Practical Applications and Use Cases
Measurement-based quantum computation (MBQC) enables practical applications like error correction and quantum simulation by leveraging cluster states for flexible resource management. Circuit-based quantum computation excels in algorithm implementation for cryptography and optimization, benefiting from well-established gate operations and hardware compatibility. Both models find use in quantum chemistry and machine learning, with MBQC offering adaptability in noise resilience and circuit-based quantum computing providing precise control over computational sequences.
Future Directions and Hybrid Quantum Computing Approaches
Measurement-based quantum computation (MBQC) leverages entangled resource states like cluster states, offering advantages in error correction and scalability compared to circuit-based models. Future directions include integrating MBQC with circuit-based quantum computing to exploit their complementary strengths, enabling more robust and flexible quantum algorithms. Hybrid quantum computing approaches seek to combine MBQC's resource-efficient measurement protocols with gate-based circuits to achieve improved fault tolerance and practical implementations on near-term quantum devices.
measurement-based quantum computation vs circuit-based quantum computation Infographic
 techiny.com
techiny.com