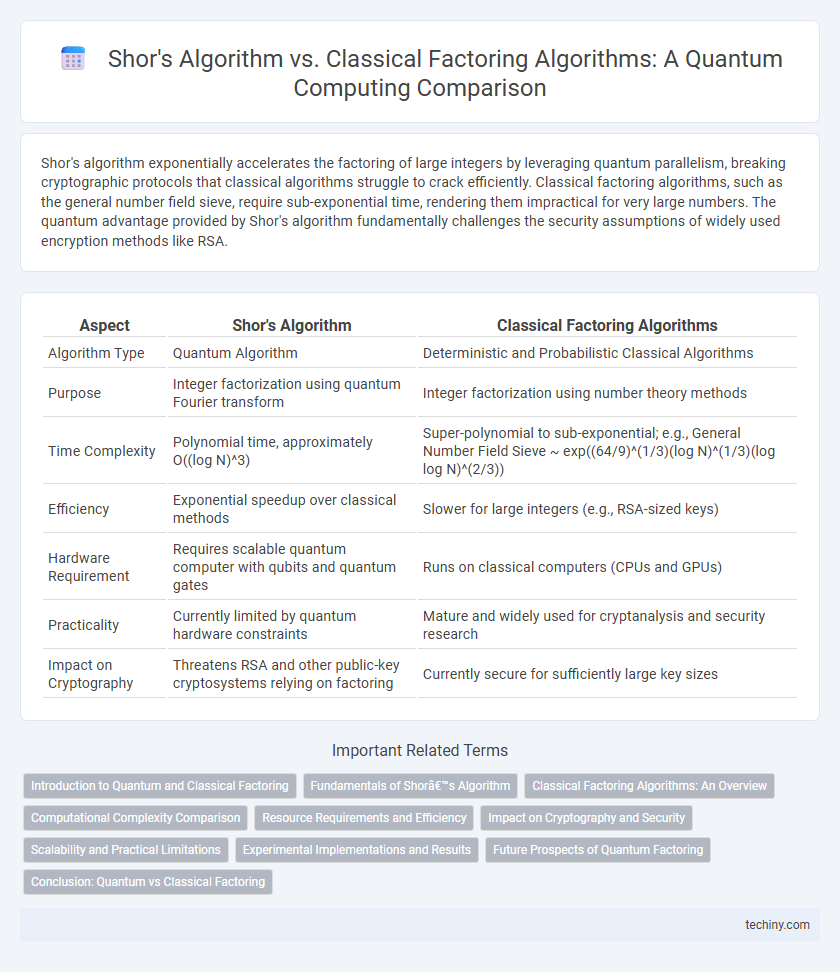
Shor's algorithm exponentially accelerates the factoring of large integers by leveraging quantum parallelism, breaking cryptographic protocols that classical algorithms struggle to crack efficiently. Classical factoring algorithms, such as the general number field sieve, require sub-exponential time, rendering them impractical for very large numbers. The quantum advantage provided by Shor's algorithm fundamentally challenges the security assumptions of widely used encryption methods like RSA.
Table of Comparison
| Aspect | Shor's Algorithm | Classical Factoring Algorithms |
|---|---|---|
| Algorithm Type | Quantum Algorithm | Deterministic and Probabilistic Classical Algorithms |
| Purpose | Integer factorization using quantum Fourier transform | Integer factorization using number theory methods |
| Time Complexity | Polynomial time, approximately O((log N)^3) | Super-polynomial to sub-exponential; e.g., General Number Field Sieve ~ exp((64/9)^(1/3)(log N)^(1/3)(log log N)^(2/3)) |
| Efficiency | Exponential speedup over classical methods | Slower for large integers (e.g., RSA-sized keys) |
| Hardware Requirement | Requires scalable quantum computer with qubits and quantum gates | Runs on classical computers (CPUs and GPUs) |
| Practicality | Currently limited by quantum hardware constraints | Mature and widely used for cryptanalysis and security research |
| Impact on Cryptography | Threatens RSA and other public-key cryptosystems relying on factoring | Currently secure for sufficiently large key sizes |
Introduction to Quantum and Classical Factoring
Shor's algorithm revolutionizes integer factorization by exploiting quantum superposition and entanglement to solve the problem exponentially faster than classical algorithms like the General Number Field Sieve (GNFS). Classical factoring algorithms rely on the computationally intensive process of trial division and sieve-based methods, which scale super-polynomially with input size, making them impractical for large integers. Quantum factoring leverages periodicity finding in the quantum Fourier transform, fundamentally outpacing classical approaches and threatening the security of widely used cryptographic systems such as RSA.
Fundamentals of Shor’s Algorithm
Shor's Algorithm leverages quantum parallelism and the quantum Fourier transform to factor large integers exponentially faster than classical algorithms such as the general number field sieve. It exploits the periodicity in modular exponentiation through quantum phase estimation, enabling the efficient determination of factors. This fundamental quantum advantage challenges the security of classical cryptographic systems based on integer factorization.
Classical Factoring Algorithms: An Overview
Classical factoring algorithms, such as the General Number Field Sieve (GNFS), remain the most efficient methods for factoring large integers on classical computers, with GNFS having a sub-exponential time complexity of approximately \(O\left(\exp\left((64/9)^{1/3}(\log N)^{1/3}(\log \log N)^{2/3}\right)\right)\). These algorithms rely on advanced number theory techniques and integer relations, making them suitable for factoring numbers up to several hundred digits, though their performance dramatically decreases as the integer size grows. Despite continuous improvements, classical methods cannot compete with Shor's algorithm's polynomial-time efficiency on sufficiently powerful quantum hardware.
Computational Complexity Comparison
Shor's algorithm revolutionizes integer factorization by operating in polynomial time, specifically O((log N)^3), compared to classical factoring algorithms such as the General Number Field Sieve, which run in sub-exponential time exp((c + o(1))(log N)^{1/3}(log log N)^{2/3}). This exponential speedup is critical for breaking widely used cryptographic schemes like RSA, which rely on the computational difficulty of factoring large integers. Quantum computing's ability to implement Shor's algorithm efficiently underscores its transformative impact on cryptanalysis and computational complexity theory.
Resource Requirements and Efficiency
Shor's algorithm dramatically reduces the computational complexity of factoring large integers, operating in polynomial time using quantum bits (qubits) compared to the exponential time required by classical factoring algorithms like the General Number Field Sieve (GNFS). Quantum resources needed for Shor's algorithm include thousands of logical qubits and error-corrected quantum gates, which present significant physical and engineering challenges. In contrast, classical algorithms demand extensive CPU time and memory scaling exponentially with input size, making them infeasible for very large integers.
Impact on Cryptography and Security
Shor's Algorithm, leveraging quantum computing, exponentially accelerates the factorization of large integers compared to classical factoring algorithms, which operate in sub-exponential time. This quantum speedup poses a significant threat to cryptographic systems based on integer factorization, such as RSA, potentially rendering them insecure against quantum attacks. As a result, the development of quantum-resistant cryptographic protocols has become crucial to maintaining data security in the post-quantum era.
Scalability and Practical Limitations
Shor's Algorithm exponentially outperforms classical factoring algorithms like the General Number Field Sieve in scalability by efficiently factoring large integers using quantum parallelism. However, practical limitations include the requirement for a fault-tolerant quantum computer with thousands of qubits, which remains beyond current hardware capabilities. Classical algorithms, while slower at large scales, benefit from mature, widely available technology and error-resilient implementations.
Experimental Implementations and Results
Experimental implementations of Shor's Algorithm on quantum processors have demonstrated the ability to factor small integers such as 15 and 21, showcasing quantum speedup potential compared to classical factoring methods like the general number field sieve. Classical algorithms remain more efficient for large-scale factoring due to current quantum hardware limitations, including qubit coherence and error rates. Advances in quantum error correction and scalable qubit systems aim to bridge this gap and enable practical quantum advantage in factoring.
Future Prospects of Quantum Factoring
Shor's Algorithm offers an exponential speedup over classical factoring algorithms by efficiently decomposing large integers using quantum Fourier transforms, which classical methods struggle to achieve in polynomial time. The future prospects of quantum factoring include breaking widely used cryptographic systems, such as RSA, by rapidly solving integer factorization problems that underpin their security. Continued advancements in quantum hardware and error correction techniques are critical to realizing practical quantum factoring and revolutionizing data security and encryption protocols.
Conclusion: Quantum vs Classical Factoring
Shor's algorithm exponentially outperforms classical factoring algorithms like the General Number Field Sieve by reducing integer factorization complexity from sub-exponential to polynomial time. Quantum factoring demonstrates potential to break widely used cryptographic protocols such as RSA, posing significant implications for cybersecurity. Classical methods remain practical for current computational limits, but quantum advancements necessitate urgent development of quantum-resistant cryptography.
Shor’s Algorithm vs Classical Factoring Algorithm Infographic
 techiny.com
techiny.com