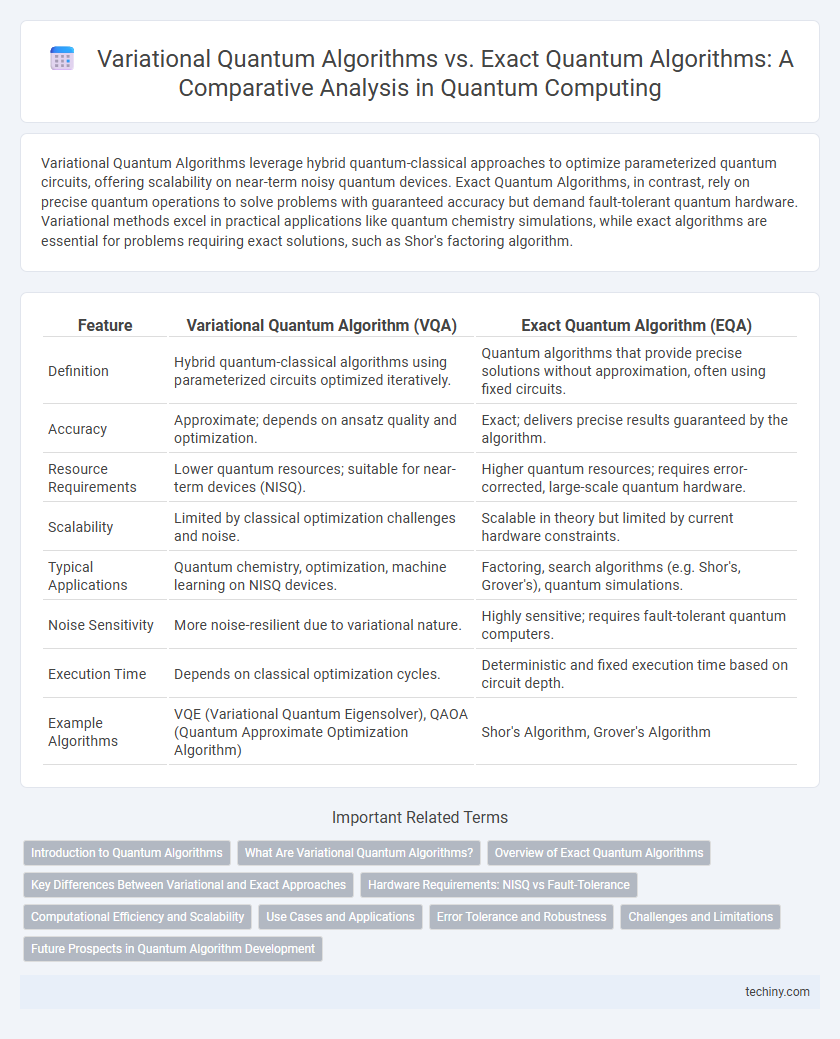
Variational Quantum Algorithms leverage hybrid quantum-classical approaches to optimize parameterized quantum circuits, offering scalability on near-term noisy quantum devices. Exact Quantum Algorithms, in contrast, rely on precise quantum operations to solve problems with guaranteed accuracy but demand fault-tolerant quantum hardware. Variational methods excel in practical applications like quantum chemistry simulations, while exact algorithms are essential for problems requiring exact solutions, such as Shor's factoring algorithm.
Table of Comparison
| Feature | Variational Quantum Algorithm (VQA) | Exact Quantum Algorithm (EQA) |
|---|---|---|
| Definition | Hybrid quantum-classical algorithms using parameterized circuits optimized iteratively. | Quantum algorithms that provide precise solutions without approximation, often using fixed circuits. |
| Accuracy | Approximate; depends on ansatz quality and optimization. | Exact; delivers precise results guaranteed by the algorithm. |
| Resource Requirements | Lower quantum resources; suitable for near-term devices (NISQ). | Higher quantum resources; requires error-corrected, large-scale quantum hardware. |
| Scalability | Limited by classical optimization challenges and noise. | Scalable in theory but limited by current hardware constraints. |
| Typical Applications | Quantum chemistry, optimization, machine learning on NISQ devices. | Factoring, search algorithms (e.g. Shor's, Grover's), quantum simulations. |
| Noise Sensitivity | More noise-resilient due to variational nature. | Highly sensitive; requires fault-tolerant quantum computers. |
| Execution Time | Depends on classical optimization cycles. | Deterministic and fixed execution time based on circuit depth. |
| Example Algorithms | VQE (Variational Quantum Eigensolver), QAOA (Quantum Approximate Optimization Algorithm) | Shor's Algorithm, Grover's Algorithm |
Introduction to Quantum Algorithms
Variational Quantum Algorithms (VQAs) leverage classical optimization techniques combined with quantum circuits to approximate solutions for complex problems, making them suitable for near-term noisy quantum devices. Exact Quantum Algorithms, such as Shor's algorithm and Grover's algorithm, provide precise solutions through deterministic quantum circuit designs but typically require fault-tolerant quantum hardware. The introduction to quantum algorithms emphasizes the trade-off between the scalability of VQAs and the exactness of traditional quantum algorithms in the evolving landscape of quantum computing.
What Are Variational Quantum Algorithms?
Variational Quantum Algorithms (VQAs) leverage a hybrid quantum-classical approach, combining parameterized quantum circuits with classical optimization to solve complex problems efficiently on noisy intermediate-scale quantum (NISQ) devices. Unlike Exact Quantum Algorithms, which require fault-tolerant quantum computers and precise gate operations, VQAs are designed to tolerate noise and hardware limitations through iterative parameter tuning and cost function minimization. VQAs are especially suited for applications such as quantum chemistry, combinatorial optimization, and machine learning, where approximate solutions offer significant computational advantages.
Overview of Exact Quantum Algorithms
Exact quantum algorithms provide precise solutions by leveraging quantum parallelism and interference, often solving problems exponentially faster than classical counterparts. Notable examples include Shor's algorithm for integer factorization and Grover's algorithm for unstructured search, both demonstrating clear quantum advantage. These algorithms rely on well-defined quantum circuits and unitary transformations, offering deterministic results within polynomial or sub-exponential time frames for specific problem classes.
Key Differences Between Variational and Exact Approaches
Variational Quantum Algorithms (VQAs) leverage parameterized quantum circuits optimized through classical feedback loops, offering scalability and robustness on near-term noisy quantum devices, contrasted with Exact Quantum Algorithms that require precise, fault-tolerant quantum operations and full quantum coherence. VQAs approximate solutions to complex problems like quantum chemistry or combinatorial optimization by minimizing a cost function, while Exact Algorithms perform deterministic, error-free computations to solve problems like Shor's or Grover's algorithms with guaranteed accuracy. The key difference lies in VQAs' hybrid quantum-classical optimization trade-off, enabling practical use on current hardware, whereas Exact Algorithms demand ideal conditions, limiting their immediate applicability.
Hardware Requirements: NISQ vs Fault-Tolerance
Variational Quantum Algorithms (VQAs) are designed to operate effectively on Noisy Intermediate-Scale Quantum (NISQ) devices, requiring fewer qubits and tolerating higher noise levels through iterative classical optimization. Exact Quantum Algorithms demand fault-tolerant quantum hardware with error correction capabilities to maintain coherence and execute precise quantum gate sequences over longer durations. The hardware constraint differences highlight VQAs' near-term applicability versus exact algorithms' dependence on future, scalable, error-corrected quantum computers.
Computational Efficiency and Scalability
Variational Quantum Algorithms (VQAs) demonstrate superior computational efficiency by leveraging classical-quantum hybrid optimization to approximate solutions with fewer qubits and shallower circuits compared to Exact Quantum Algorithms, which require full quantum state representations often leading to exponential resource demands. Scalability in VQAs benefits from adaptive parameter tuning and noise resilience, enabling practical implementation on near-term noisy intermediate-scale quantum (NISQ) devices, whereas Exact Quantum Algorithms face significant challenges scaling beyond small qubit systems due to coherence time limitations and hardware error rates. This contrast positions VQAs as more viable for solving complex, large-scale problems on current quantum hardware platforms.
Use Cases and Applications
Variational Quantum Algorithms (VQAs) excel in solving optimization problems, quantum chemistry simulations, and machine learning tasks on noisy intermediate-scale quantum (NISQ) devices due to their adaptability and reduced circuit depth. Exact Quantum Algorithms, such as Shor's or Grover's algorithms, deliver precise solutions for factoring and unstructured search but require fully error-corrected quantum computers, making them suitable for cryptography and database applications in the long term. VQAs are preferred for near-term practical applications where hardware limitations exist, whereas exact algorithms target high-precision, large-scale quantum advantage scenarios.
Error Tolerance and Robustness
Variational Quantum Algorithms (VQAs) exhibit higher error tolerance and robustness compared to Exact Quantum Algorithms by leveraging parameter optimization and hybrid quantum-classical feedback loops that mitigate noise effects. Exact Quantum Algorithms require near-perfect qubits and low error rates due to their reliance on precise gate operations without iterative error correction, making them less resilient to decoherence and operational errors. Consequently, VQAs are more practical for current noisy intermediate-scale quantum (NISQ) devices, offering improved robustness against hardware imperfections.
Challenges and Limitations
Variational Quantum Algorithms face challenges in scalability and noise sensitivity, limiting their application on current noisy intermediate-scale quantum (NISQ) devices. Exact Quantum Algorithms require fault-tolerant quantum hardware, which remains technologically unavailable, restricting their practical implementation. Both approaches encounter difficulties with quantum error correction and resource demands, constraining their efficacy in solving large-scale problems.
Future Prospects in Quantum Algorithm Development
Variational Quantum Algorithms (VQAs) offer scalable solutions for near-term quantum devices by leveraging hybrid quantum-classical optimization to tackle complex problems with reduced quantum resource demands. Exact Quantum Algorithms provide precise solutions but require fully error-corrected quantum systems, limiting their near-term applicability. Future quantum algorithm development will likely integrate VQAs' adaptability with advances in error correction, enhancing performance across a broader range of applications in chemistry, optimization, and machine learning.
Variational Quantum Algorithm vs Exact Quantum Algorithm Infographic
 techiny.com
techiny.com