Adiabatic quantum computation leverages the gradual evolution of a quantum system's ground state to solve optimization problems by encoding solutions in energy landscapes, offering robustness against certain types of errors. Digital quantum computation relies on discrete quantum gates to manipulate qubits through precise sequences, enabling universal quantum algorithms and greater flexibility in problem solving. Comparing both, adiabatic approaches excel in specific optimization tasks while digital quantum computers provide broader applicability across diverse quantum algorithms.
Table of Comparison
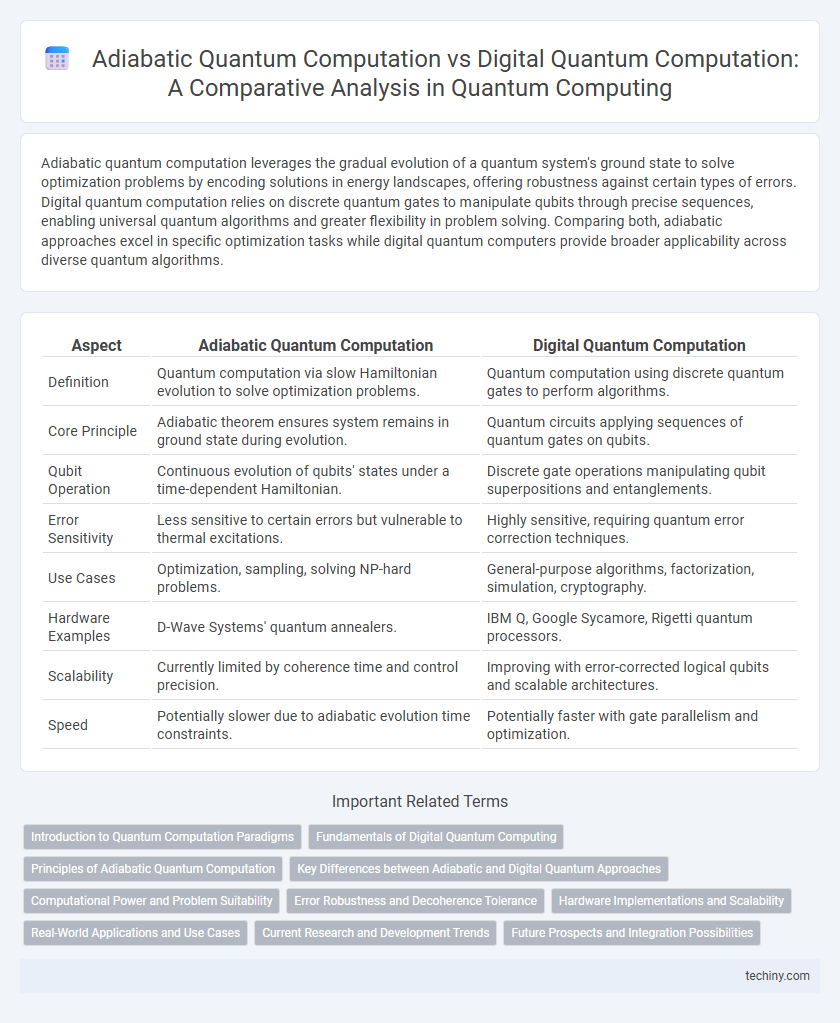
| Aspect | Adiabatic Quantum Computation | Digital Quantum Computation |
|---|---|---|
| Definition | Quantum computation via slow Hamiltonian evolution to solve optimization problems. | Quantum computation using discrete quantum gates to perform algorithms. |
| Core Principle | Adiabatic theorem ensures system remains in ground state during evolution. | Quantum circuits applying sequences of quantum gates on qubits. |
| Qubit Operation | Continuous evolution of qubits' states under a time-dependent Hamiltonian. | Discrete gate operations manipulating qubit superpositions and entanglements. |
| Error Sensitivity | Less sensitive to certain errors but vulnerable to thermal excitations. | Highly sensitive, requiring quantum error correction techniques. |
| Use Cases | Optimization, sampling, solving NP-hard problems. | General-purpose algorithms, factorization, simulation, cryptography. |
| Hardware Examples | D-Wave Systems' quantum annealers. | IBM Q, Google Sycamore, Rigetti quantum processors. |
| Scalability | Currently limited by coherence time and control precision. | Improving with error-corrected logical qubits and scalable architectures. |
| Speed | Potentially slower due to adiabatic evolution time constraints. | Potentially faster with gate parallelism and optimization. |
Introduction to Quantum Computation Paradigms
Adiabatic quantum computation leverages the gradual evolution of a quantum system's ground state to solve optimization problems, contrasting with digital quantum computation's use of discrete quantum gates for algorithm execution. The adiabatic model relies on the quantum adiabatic theorem to ensure the system remains in its lowest energy state, offering robustness against certain types of errors and noise. Digital quantum computation, central to gate-based quantum algorithms like Shor's and Grover's, emphasizes precise control of quantum bits through a sequence of logic gates, enabling versatile quantum algorithm implementation.
Fundamentals of Digital Quantum Computing
Digital quantum computing relies on quantum gates to manipulate qubits through discrete operations, enabling the implementation of complex algorithms such as Shor's and Grover's algorithms. This framework utilizes a universal set of quantum gates to perform error correction and achieve scalability, making it suitable for a wide range of computational problems. Fundamental components include the quantum circuit model, superposition, entanglement, and measurement, which form the basis for quantum information processing in digital systems.
Principles of Adiabatic Quantum Computation
Adiabatic Quantum Computation (AQC) relies on the principle of slowly evolving a quantum system from an initial Hamiltonian with a known ground state to a final Hamiltonian encoding the solution to a computational problem, ensuring the system remains in its ground state throughout the process. This approach contrasts with digital quantum computation, which uses discrete quantum gates to manipulate qubits in a stepwise manner. The adiabatic theorem underpins AQC, guaranteeing that if the Hamiltonian changes sufficiently slowly, the system will avoid excitations to higher energy states, making it particularly effective for optimization problems and quantum annealing tasks.
Key Differences between Adiabatic and Digital Quantum Approaches
Adiabatic quantum computation relies on slowly evolving the quantum system's Hamiltonian to solve optimization problems, while digital quantum computation uses discrete gate operations for universal quantum algorithms. Adiabatic methods excel in finding ground states of complex systems but face challenges in error correction and scalability compared to digital quantum circuits. Digital quantum computation offers greater algorithmic flexibility and fault-tolerant designs, making it more suitable for a wider range of applications beyond optimization.
Computational Power and Problem Suitability
Adiabatic quantum computation excels in solving optimization problems and certain classes of NP-hard problems by leveraging quantum annealing to find ground states of complex Hamiltonians. Digital quantum computation offers broader computational power with universal gate sets enabling implementation of diverse algorithms, including Shor's and Grover's, suitable for factoring and database search. While adiabatic models are specialized and hardware-efficient, digital quantum computers provide flexibility and scalability for a wider range of quantum algorithms.
Error Robustness and Decoherence Tolerance
Adiabatic quantum computation exhibits greater error robustness and decoherence tolerance by evolving the system slowly through its ground state, minimizing transitions to excited states and reducing susceptibility to noise. Digital quantum computation, relying on discrete gate operations, faces higher error rates due to gate imperfections and requires quantum error correction to manage decoherence effects. Consequently, adiabatic models are often preferred in noisy intermediate-scale quantum (NISQ) devices for their inherent resilience to environmental disturbances.
Hardware Implementations and Scalability
Adiabatic quantum computation relies on analog hardware implementations using quantum annealers that manipulate energy landscapes to find ground states, offering natural robustness against certain errors but limited scalability due to hardware constraints. Digital quantum computation uses gate-based quantum processors with qubits arranged in circuits, enabling universal computation and more flexible error correction strategies, yet facing scalability challenges linked to qubit coherence times and control precision. Advances in superconducting qubits and trapped ions are driving scalability improvements in digital quantum hardware, whereas adiabatic machines like D-Wave systems remain specialized for optimization tasks with gradual scalability.
Real-World Applications and Use Cases
Adiabatic quantum computation excels in solving complex optimization problems and simulating quantum systems, making it suitable for logistics, material science, and quantum chemistry applications. Digital quantum computation offers versatility with gate-based algorithms, enabling advances in cryptography, machine learning, and drug discovery. Both paradigms complement each other by addressing distinct challenges across finance, artificial intelligence, and complex system modeling.
Current Research and Development Trends
Current research in quantum computing emphasizes adiabatic quantum computation (AQC) for solving optimization problems by evolving quantum states slowly to remain in the ground state, offering robustness against certain types of errors. Digital quantum computation, meanwhile, progresses rapidly with advancements in fault-tolerant error correction, gate fidelity, and qubit coherence, enabling complex algorithm implementation on gate-based quantum processors. Hybrid approaches combining AQC's continuous adiabatic processes with digital quantum gates are emerging, aiming to leverage strengths from both paradigms for enhanced computational efficiency and scalability.
Future Prospects and Integration Possibilities
Adiabatic quantum computation offers promising prospects for solving optimization problems by evolving quantum states slowly to remain in their ground state, making it inherently robust to certain errors. Digital quantum computation, with its gate-based architecture, provides versatility and scalability through error-correcting codes and modular algorithms suited for a wide range of applications. Integration of both paradigms could leverage adiabatic methods for specialized tasks within digital quantum processors, enhancing computational efficiency and expanding the operational scope of future quantum technologies.
adiabatic quantum computation vs digital quantum computation Infographic
 techiny.com
techiny.com