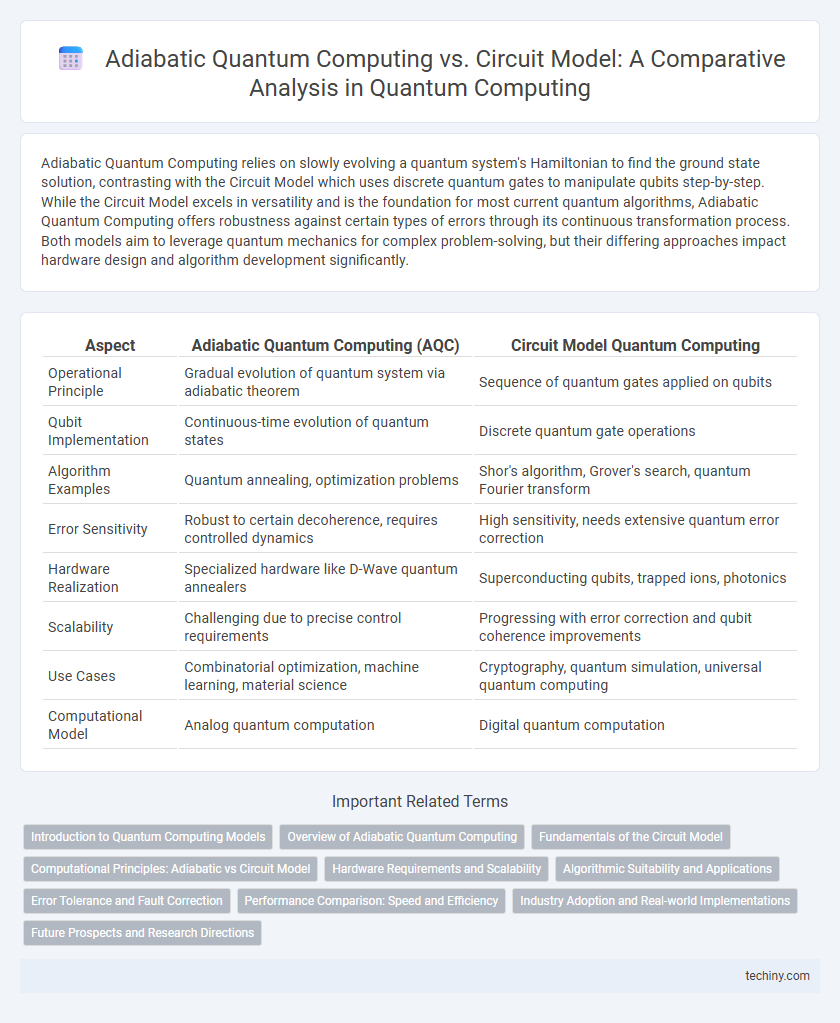
Adiabatic Quantum Computing relies on slowly evolving a quantum system's Hamiltonian to find the ground state solution, contrasting with the Circuit Model which uses discrete quantum gates to manipulate qubits step-by-step. While the Circuit Model excels in versatility and is the foundation for most current quantum algorithms, Adiabatic Quantum Computing offers robustness against certain types of errors through its continuous transformation process. Both models aim to leverage quantum mechanics for complex problem-solving, but their differing approaches impact hardware design and algorithm development significantly.
Table of Comparison
| Aspect | Adiabatic Quantum Computing (AQC) | Circuit Model Quantum Computing |
|---|---|---|
| Operational Principle | Gradual evolution of quantum system via adiabatic theorem | Sequence of quantum gates applied on qubits |
| Qubit Implementation | Continuous-time evolution of quantum states | Discrete quantum gate operations |
| Algorithm Examples | Quantum annealing, optimization problems | Shor's algorithm, Grover's search, quantum Fourier transform |
| Error Sensitivity | Robust to certain decoherence, requires controlled dynamics | High sensitivity, needs extensive quantum error correction |
| Hardware Realization | Specialized hardware like D-Wave quantum annealers | Superconducting qubits, trapped ions, photonics |
| Scalability | Challenging due to precise control requirements | Progressing with error correction and qubit coherence improvements |
| Use Cases | Combinatorial optimization, machine learning, material science | Cryptography, quantum simulation, universal quantum computing |
| Computational Model | Analog quantum computation | Digital quantum computation |
Introduction to Quantum Computing Models
Adiabatic quantum computing (AQC) employs continuous-time evolution of a quantum system's Hamiltonian to solve optimization problems by encoding solutions into the system's ground state, contrasting with the circuit model that utilizes discrete quantum gates to perform algorithms on qubits. The circuit model, foundational for universal quantum computation, relies on sequences of unitary operations and measurement, while AQC leverages the adiabatic theorem to maintain the system in its lowest energy state during gradual transformations. Both models represent distinct approaches to harnessing quantum mechanics, with AQC often favored for combinatorial optimization and the circuit model underpinning most quantum algorithm implementations like Shor's and Grover's algorithms.
Overview of Adiabatic Quantum Computing
Adiabatic Quantum Computing (AQC) leverages the principles of quantum annealing by slowly evolving the quantum state of a system from an initial Hamiltonian to a problem-specific final Hamiltonian, ensuring the system remains in its ground state to find optimal solutions. Unlike the circuit model, which relies on sequences of quantum gates applied in discrete steps, AQC encodes the solution in the lowest energy state of a problem Hamiltonian, making it particularly effective for optimization and combinatorial problems. The robustness of AQC against certain types of quantum decoherence offers potential advantages in scalability and implementation on current quantum hardware architectures.
Fundamentals of the Circuit Model
The circuit model of quantum computing relies on quantum bits (qubits) manipulated through a sequence of quantum gates, enabling universal quantum computation by decomposing complex algorithms into elementary gate operations. This model uses quantum circuits composed of single-qubit rotations and multi-qubit entangling gates, allowing precise control over quantum states and enabling error correction techniques. Its fundamental advantage lies in the ability to implement a wide range of quantum algorithms through well-defined gate sets and circuit depth optimization.
Computational Principles: Adiabatic vs Circuit Model
Adiabatic quantum computing (AQC) operates by encoding the solution to a problem in the ground state of a slowly evolving Hamiltonian, relying on the adiabatic theorem to maintain the system in its lowest energy state. In contrast, the circuit model of quantum computing uses a sequence of quantum gates applied to qubits, facilitating dynamic state manipulation through unitary operations. AQC emphasizes energy landscape evolution and minimal transitions between states, whereas the circuit model prioritizes discrete gate-based transformations and quantum algorithms like Shor's and Grover's.
Hardware Requirements and Scalability
Adiabatic Quantum Computing (AQC) utilizes quantum annealers with hardware optimized for continuous parameter tuning and energy gap preservation, requiring fewer qubits with robust coherence times, while Circuit Model Quantum Computing demands complex gate operations on highly coherent qubits with extensive error correction protocols. Scalability challenges in AQC stem from maintaining adiabatic conditions over larger problem sizes, whereas Circuit Model systems face overhead due to gate fidelity and error correction as qubit numbers increase. Advances in superconducting qubits and annealing technology influence the trade-offs in hardware complexity and scalability between these two quantum computing models.
Algorithmic Suitability and Applications
Adiabatic Quantum Computing (AQC) excels in solving optimization problems and discrete combinatorial tasks by gradually evolving the quantum state, making it suitable for algorithms like quantum annealing and quantum approximate optimization. The Circuit Model of quantum computing offers greater flexibility for implementing a wide range of quantum algorithms, including Shor's factoring and Grover's search, by utilizing gate-based operations on qubits. While AQC is inherently robust against certain types of errors in optimization contexts, the Circuit Model supports more complex algorithmic structures and error correction techniques, enabling broader applications across cryptography, simulation, and general-purpose quantum computing.
Error Tolerance and Fault Correction
Adiabatic Quantum Computing (AQC) inherently suppresses certain types of errors through gradual evolution, providing higher error tolerance in analog implementations compared to the Circuit Model. The Circuit Model relies heavily on quantum error correction codes, such as surface codes, to manage decoherence and gate errors, making fault-tolerant operations feasible but resource-intensive. Error correction in AQC remains a significant challenge due to fewer established fault-tolerant protocols, limiting its scalability compared to the well-developed error correction techniques in the Circuit Model.
Performance Comparison: Speed and Efficiency
Adiabatic quantum computing excels in solving optimization problems by evolving the ground state slowly, often leading to better energy efficiency but slower execution compared to circuit model quantum computing. Circuit model systems leverage gate-based operations for faster algorithmic implementation, showing superior speed in executing complex tasks like factoring and quantum simulation. Performance comparisons reveal that while circuit models offer higher speed, adiabatic approaches provide robustness and potential efficiency gains in specific problem domains.
Industry Adoption and Real-world Implementations
Adiabatic Quantum Computing (AQC) has gained traction in industries like logistics and finance due to its suitability for optimization problems, with companies like D-Wave Systems leading real-world deployments. The Circuit Model, exemplified by IBM Q and Google's Sycamore, dominates broader quantum computing applications, including error correction and algorithm development, attracting substantial investment from tech giants and academic institutions. Industry adoption trends reveal AQC's niche use cases, while the Circuit Model's versatility drives extensive research and commercial quantum software ecosystems.
Future Prospects and Research Directions
Adiabatic Quantum Computing (AQC) demonstrates promising advantages in solving optimization problems through quantum annealing, with ongoing research focused on enhancing qubit coherence and scalability compared to the circuit model. Circuit-based quantum computing benefits from a more mature theoretical foundation and error correction protocols, driving advancements in universal gate operations and fault-tolerant architectures. Future research will likely explore hybrid approaches integrating AQC and circuit models to leverage their complementary strengths for scalable, practical quantum algorithms.
Adiabatic Quantum Computing vs Circuit Model Infographic
 techiny.com
techiny.com