State tomography reconstructs the quantum state by measuring multiple copies and analyzing their outcomes, enabling accurate characterization of qubits. Process tomography, on the other hand, maps the complete quantum operation or channel, providing insight into how quantum states evolve under specific transformations. Both techniques are essential for validating quantum devices, but state tomography focuses on static state identification while process tomography captures dynamic process behavior.
Table of Comparison
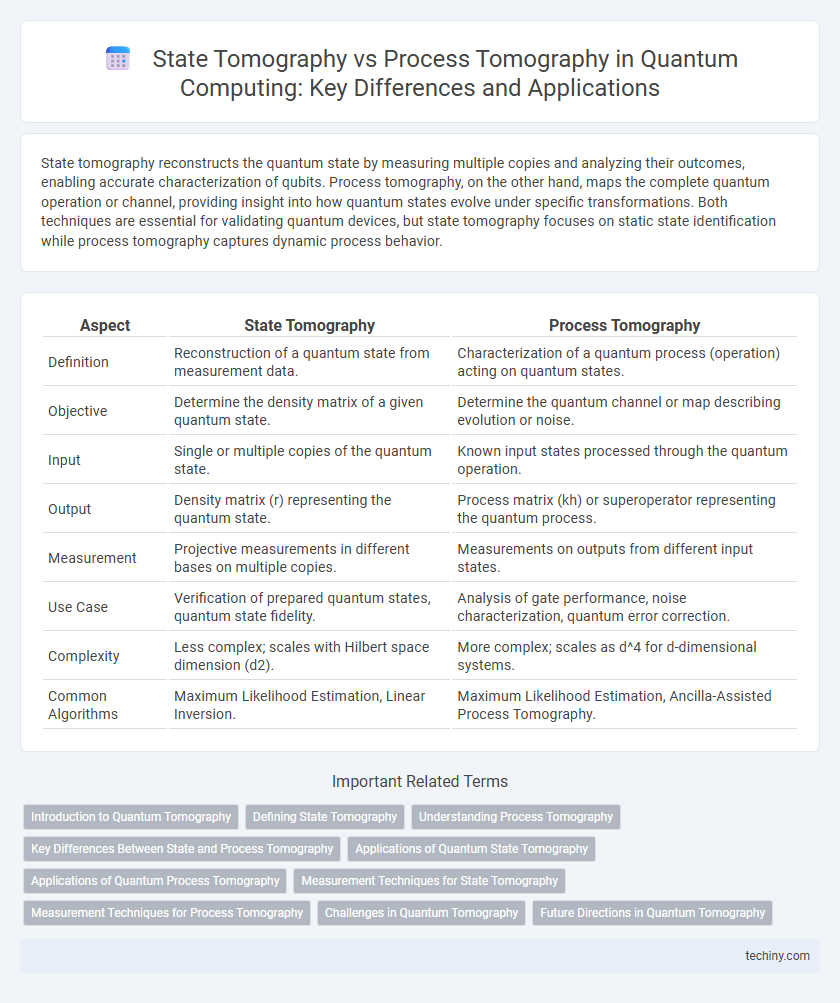
| Aspect | State Tomography | Process Tomography |
|---|---|---|
| Definition | Reconstruction of a quantum state from measurement data. | Characterization of a quantum process (operation) acting on quantum states. |
| Objective | Determine the density matrix of a given quantum state. | Determine the quantum channel or map describing evolution or noise. |
| Input | Single or multiple copies of the quantum state. | Known input states processed through the quantum operation. |
| Output | Density matrix (r) representing the quantum state. | Process matrix (kh) or superoperator representing the quantum process. |
| Measurement | Projective measurements in different bases on multiple copies. | Measurements on outputs from different input states. |
| Use Case | Verification of prepared quantum states, quantum state fidelity. | Analysis of gate performance, noise characterization, quantum error correction. |
| Complexity | Less complex; scales with Hilbert space dimension (d2). | More complex; scales as d^4 for d-dimensional systems. |
| Common Algorithms | Maximum Likelihood Estimation, Linear Inversion. | Maximum Likelihood Estimation, Ancilla-Assisted Process Tomography. |
Introduction to Quantum Tomography
Quantum tomography encompasses techniques for reconstructing quantum states and processes from measurement data, essential for characterizing quantum systems. State tomography aims to determine the density matrix representing a quantum state's probabilities and coherences, while process tomography characterizes quantum operations by mapping input states to output states. Both approaches require carefully designed measurement settings and statistical methods to achieve accurate and reliable reconstruction in quantum computing.
Defining State Tomography
State tomography is the technique used to reconstruct the full quantum state of a system by performing a series of measurements on multiple identically prepared copies, enabling the determination of the system's density matrix. It provides detailed information about the probabilities and coherences of quantum states, essential for characterizing quantum bits (qubits) in quantum computing experiments. In contrast, process tomography aims to characterize the quantum operation or channel by analyzing its effect on various input states rather than the state itself.
Understanding Process Tomography
Process tomography characterizes quantum operations by reconstructing a quantum process's complete mathematical description, enabling the analysis of noise and errors in quantum gates. It involves preparing a set of input states, applying the quantum process, and measuring the output states using state tomography techniques to infer the process matrix or superoperator. This method provides critical insights into the fidelity and dynamics of quantum channels, crucial for optimizing quantum circuits and error correction protocols.
Key Differences Between State and Process Tomography
State tomography reconstructs the quantum state's density matrix by measuring multiple copies of the same quantum system, enabling the characterization of individual quantum states. Process tomography, in contrast, determines the complete description of a quantum operation or channel by analyzing its effect on a set of input states, providing insights into the dynamics and errors of quantum gates. The key difference lies in state tomography focusing on the properties of quantum states, while process tomography characterizes the transformations applied to those states within quantum computing systems.
Applications of Quantum State Tomography
Quantum state tomography enables precise reconstruction of quantum states, which is essential for validating qubit initialization and quantum gate fidelity in quantum computing experiments. It plays a critical role in benchmarking quantum devices by providing detailed information about the density matrix of qubits. This technique supports error correction protocols and quantum algorithm development by offering a comprehensive understanding of the quantum system's state.
Applications of Quantum Process Tomography
Quantum process tomography (QPT) is essential for characterizing quantum operations by reconstructing the complete description of quantum channels, enabling error diagnosis and correction in quantum computing systems. QPT applications include verifying the performance of quantum gates, optimizing quantum circuits, and benchmarking noise and decoherence effects in quantum processors. These capabilities are crucial for advancing fault-tolerant quantum computing and improving the accuracy of quantum algorithms.
Measurement Techniques for State Tomography
Measurement techniques for state tomography primarily involve projective measurements on multiple copies of the quantum state to reconstruct its density matrix. Methods such as quantum state reconstruction leverage Pauli operator measurements or informationally complete positive operator-valued measures (POVMs) to capture the full quantum state information. These measurements enable accurate characterization of quantum states, critical for validating quantum circuits and algorithms in quantum computing.
Measurement Techniques for Process Tomography
Process tomography relies on a comprehensive set of measurement techniques to accurately reconstruct the quantum operation, including complete positive maps. These measurements involve preparing a variety of input states and performing quantum state tomography on the outputs to gather sufficient data for characterizing the process. Advanced methods, such as compressed sensing and adaptive measurement protocols, enhance efficiency and precision in determining the underlying quantum channels.
Challenges in Quantum Tomography
Quantum state tomography faces challenges such as exponential scaling in the number of measurements required for accurately reconstructing the quantum state, making it resource-intensive for large qubit systems. Process tomography increases complexity further by needing to characterize quantum channels or operations, demanding comprehensive sets of input states and measurements. Both methods struggle with noise sensitivity, error accumulation, and computational demands, posing significant hurdles for practical quantum system characterization.
Future Directions in Quantum Tomography
Emerging advancements in quantum tomography emphasize enhancing efficiency and accuracy in both state and process tomography through machine learning algorithms and adaptive measurement protocols. Future directions target scalable tomography techniques capable of characterizing high-dimensional quantum systems, leveraging compressed sensing and neural networks to reduce the exponential resource overhead. Integration of real-time error mitigation and robust noise modeling promises to significantly improve the practicality of quantum tomography in complex quantum computing architectures.
state tomography vs process tomography Infographic
 techiny.com
techiny.com