QAOA targets combinatorial optimization problems by leveraging parameterized quantum circuits to approximate solutions through iterative classical-quantum feedback loops. VQE primarily aims to find ground state energies of molecular systems by minimizing the expectation value of a Hamiltonian using a hybrid quantum-classical approach. Both algorithms utilize variational principles but differ in application scope, with QAOA tailored for discrete optimization and VQE designed for chemistry and materials science challenges.
Table of Comparison
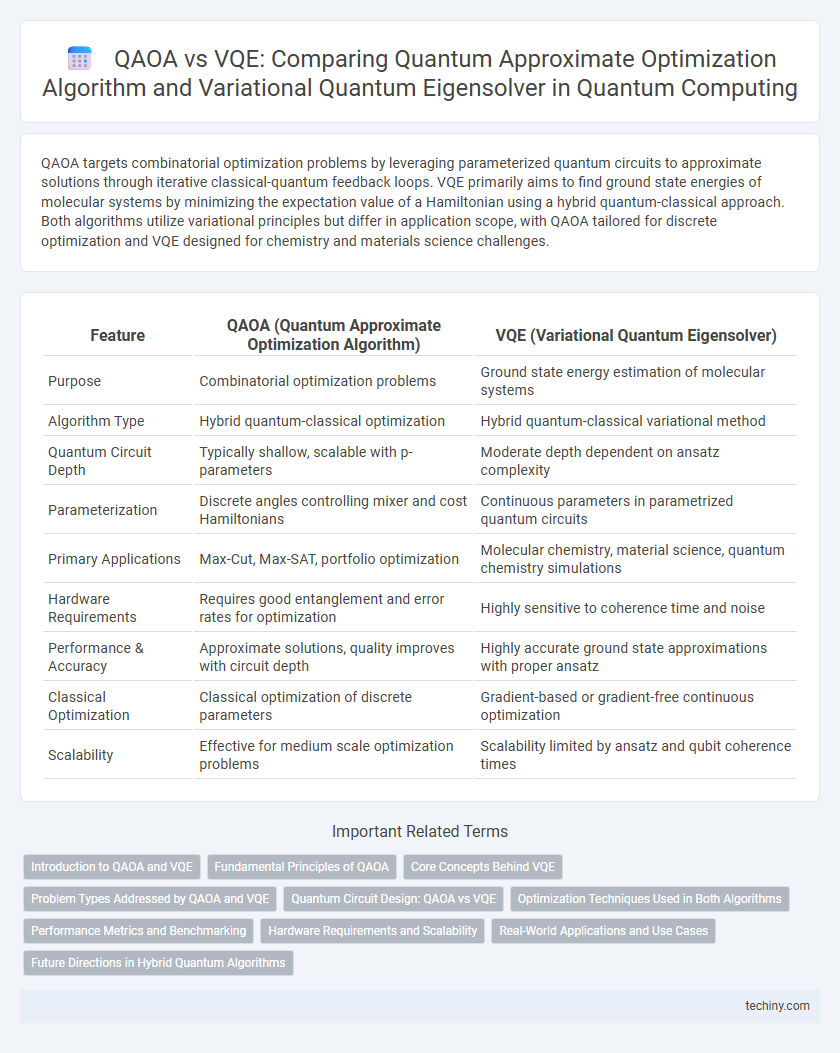
| Feature | QAOA (Quantum Approximate Optimization Algorithm) | VQE (Variational Quantum Eigensolver) |
|---|---|---|
| Purpose | Combinatorial optimization problems | Ground state energy estimation of molecular systems |
| Algorithm Type | Hybrid quantum-classical optimization | Hybrid quantum-classical variational method |
| Quantum Circuit Depth | Typically shallow, scalable with p-parameters | Moderate depth dependent on ansatz complexity |
| Parameterization | Discrete angles controlling mixer and cost Hamiltonians | Continuous parameters in parametrized quantum circuits |
| Primary Applications | Max-Cut, Max-SAT, portfolio optimization | Molecular chemistry, material science, quantum chemistry simulations |
| Hardware Requirements | Requires good entanglement and error rates for optimization | Highly sensitive to coherence time and noise |
| Performance & Accuracy | Approximate solutions, quality improves with circuit depth | Highly accurate ground state approximations with proper ansatz |
| Classical Optimization | Classical optimization of discrete parameters | Gradient-based or gradient-free continuous optimization |
| Scalability | Effective for medium scale optimization problems | Scalability limited by ansatz and qubit coherence times |
Introduction to QAOA and VQE
QAOA (Quantum Approximate Optimization Algorithm) is designed to solve combinatorial optimization problems by leveraging parameterized quantum circuits to approximate the ground state of problem-specific Hamiltonians. VQE (Variational Quantum Eigensolver) uses a hybrid quantum-classical approach to find the lowest eigenvalue of Hamiltonians, primarily applied in quantum chemistry and material science for molecular energy estimation. Both algorithms use variational principles but target different problem domains, with QAOA focusing on discrete optimization and VQE on continuous eigenvalue problems.
Fundamental Principles of QAOA
QAOA leverages a parameterized quantum circuit designed to approximate combinatorial optimization problems by alternating between problem-specific and mixing Hamiltonians, effectively navigating the solution space. It fundamentally exploits the principles of quantum superposition and interference to enhance solution probabilities for optimization tasks. Unlike VQE, which targets ground-state energy estimation of molecular systems, QAOA is tailored for discrete optimization via a structured sequence of parameter updates guided by a classical optimizer.
Core Concepts Behind VQE
VQE (Variational Quantum Eigensolver) leverages a hybrid quantum-classical approach to estimate the ground state energy of a quantum system by variationally optimizing a parameterized quantum circuit. It uses a quantum processor to prepare trial wavefunctions and measures their expectation values, while a classical optimizer updates parameters to minimize energy. This approach efficiently addresses problems in quantum chemistry and materials science by approximating eigenstates within a feasible computational framework.
Problem Types Addressed by QAOA and VQE
QAOA specializes in combinatorial optimization problems such as Max-Cut, graph partitioning, and satisfiability, leveraging parametrized quantum circuits to approximate solutions efficiently. VQE, on the other hand, primarily targets quantum chemistry and materials science challenges by estimating ground state energies of molecular Hamiltonians using a hybrid quantum-classical approach. Both algorithms exploit variational principles but are optimized for distinct problem domains with QAOA excelling in discrete combinatorial tasks while VQE focuses on continuous parameter spaces in quantum systems.
Quantum Circuit Design: QAOA vs VQE
Quantum Approximate Optimization Algorithm (QAOA) employs a layered, problem-parameterized quantum circuit integrating cost and mixer Hamiltonians to approximate solutions for combinatorial optimization problems. Variational Quantum Eigensolver (VQE) utilizes parameterized quantum circuits designed to minimize the expected energy of molecular Hamiltonians, offering flexible ansatz structures like UCCSD or hardware-efficient circuits optimized for near-term quantum devices. QAOA's circuit depth scales with the number of algorithmic rounds to enhance solution quality, while VQE circuits focus on balancing circuit complexity and noise resilience for accurate ground state energy estimation.
Optimization Techniques Used in Both Algorithms
QAOA uses a parameterized quantum circuit to approximate solutions for combinatorial optimization problems by alternating between applying problem-specific and mixing Hamiltonians, optimizing parameters via classical algorithms like gradient descent to minimize cost functions. VQE employs a variational approach where a parameterized ansatz state is prepared on a quantum processor, and classical optimization algorithms iteratively adjust parameters to minimize the expected energy of a target Hamiltonian, typically solving quantum chemistry problems. Both algorithms integrate hybrid quantum-classical optimization loops, but QAOA specifically targets discrete optimization landscapes while VQE focuses on continuous energy minimization.
Performance Metrics and Benchmarking
QAOA excels in solving combinatorial optimization problems by leveraging quantum circuits tailored for approximation ratios, often benchmarked using problem-specific metrics like the Max-Cut value or approximation ratio fidelity. VQE specializes in estimating ground state energies of molecular systems, with performance assessed through convergence speed, energy error, and circuit depth efficiency. Benchmarking these algorithms requires evaluating scalability on near-term quantum hardware, noise resilience, and the quality of variational parameter optimization to determine efficacy across different quantum applications.
Hardware Requirements and Scalability
QAOA (Quantum Approximate Optimization Algorithm) typically demands fewer qubits and shallower circuit depths compared to VQE (Variational Quantum Eigensolver), making it more compatible with near-term noisy intermediate-scale quantum (NISQ) devices. VQE requires more qubits and deeper circuits to accurately approximate molecular ground states, presenting greater challenges for hardware with limited coherence times. Scalability remains more promising for QAOA in combinatorial optimization problems, whereas VQE faces bottlenecks due to increased circuit complexity and noise sensitivity as the system size grows.
Real-World Applications and Use Cases
QAOA excels in solving combinatorial optimization problems such as portfolio optimization, logistics, and scheduling by leveraging quantum superposition and interference to approximate solutions efficiently. VQE is predominantly applied in quantum chemistry and materials science for simulating molecular energies and electronic structures, enabling breakthroughs in drug discovery and catalysis. Both algorithms utilize parameterized quantum circuits but target distinct real-world challenges, with QAOA optimized for discrete optimization tasks and VQE for continuous eigenvalue problems.
Future Directions in Hybrid Quantum Algorithms
QAOA and VQE represent pivotal hybrid quantum algorithms driving quantum advantage in optimization and chemical simulations, respectively. Future research aims to enhance algorithmic scalability and error resilience by integrating adaptive parameter tuning and noise mitigation techniques. Leveraging classical-quantum feedback loops and hardware-efficient ansatzes will accelerate practical applications in material science and complex optimization problems.
QAOA (Quantum Approximate Optimization Algorithm) vs VQE (Variational Quantum Eigensolver) Infographic
 techiny.com
techiny.com