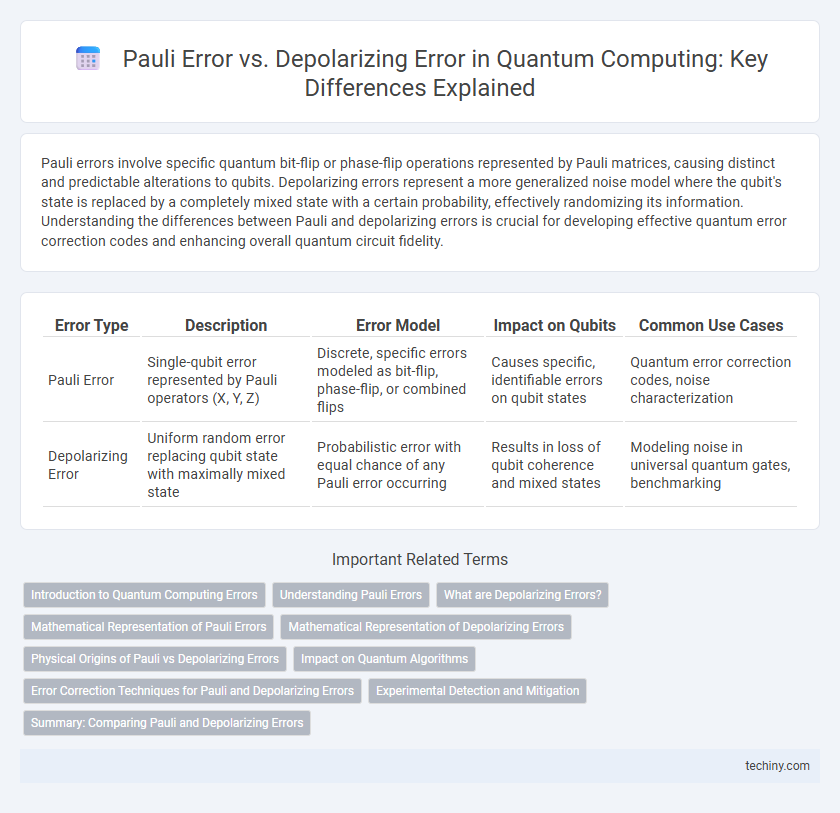
Pauli errors involve specific quantum bit-flip or phase-flip operations represented by Pauli matrices, causing distinct and predictable alterations to qubits. Depolarizing errors represent a more generalized noise model where the qubit's state is replaced by a completely mixed state with a certain probability, effectively randomizing its information. Understanding the differences between Pauli and depolarizing errors is crucial for developing effective quantum error correction codes and enhancing overall quantum circuit fidelity.
Table of Comparison
| Error Type | Description | Error Model | Impact on Qubits | Common Use Cases |
|---|---|---|---|---|
| Pauli Error | Single-qubit error represented by Pauli operators (X, Y, Z) | Discrete, specific errors modeled as bit-flip, phase-flip, or combined flips | Causes specific, identifiable errors on qubit states | Quantum error correction codes, noise characterization |
| Depolarizing Error | Uniform random error replacing qubit state with maximally mixed state | Probabilistic error with equal chance of any Pauli error occurring | Results in loss of qubit coherence and mixed states | Modeling noise in universal quantum gates, benchmarking |
Introduction to Quantum Computing Errors
Pauli errors in quantum computing correspond to bit-flip, phase-flip, or both errors represented by Pauli operators X, Z, and Y, essential in modeling error channels in qubits. Depolarizing errors describe a noise model where a qubit randomly transforms into a completely mixed state with a certain probability, effectively simulating uniform errors over the Bloch sphere. Understanding these error types is crucial for developing quantum error correction codes and improving qubit coherence in quantum processors.
Understanding Pauli Errors
Pauli errors in quantum computing refer specifically to bit-flip (X), phase-flip (Z), and combined bit-phase-flip (Y) errors, which directly correspond to Pauli matrices acting on qubits. These errors are fundamental because they form a basis for describing more complex noise processes and are crucial in error correction codes like the surface code. Understanding Pauli errors enables the decomposition of arbitrary errors into standard error syndromes, improving fault-tolerant quantum computation design.
What are Depolarizing Errors?
Depolarizing errors in quantum computing represent a noise model where a qubit's state becomes completely mixed with a certain probability, effectively losing all quantum information. This error type randomly applies one of the Pauli operators (X, Y, or Z) or leaves the qubit unchanged, resulting in uniform decoherence across the quantum state. Depolarizing errors are critical for simulating realistic quantum noise and benchmarking quantum error correction protocols.
Mathematical Representation of Pauli Errors
Pauli errors in quantum computing are mathematically represented using the Pauli matrices \(X\), \(Y\), and \(Z\), which form a basis for single-qubit error operations. Each Pauli error corresponds to a specific unitary operator acting on the qubit state, such as \(X = \begin{pmatrix}0 & 1 \\ 1 & 0\end{pmatrix}\), \(Y = \begin{pmatrix}0 & -i \\ i & 0\end{pmatrix}\), and \(Z = \begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}\). Depolarizing error is often modeled as a probabilistic mixture of these Pauli errors, represented by the quantum operation \(\mathcal{E}(\rho) = (1-p)\rho + \frac{p}{3}(X\rho X + Y\rho Y + Z\rho Z)\), where \(p\) denotes the depolarizing probability.
Mathematical Representation of Depolarizing Errors
Depolarizing errors are mathematically represented by a quantum operation that replaces the input state r with a maximally mixed state I/d with probability p, described as E(r) = (1 - p)r + (p/d)I, where d is the dimension of the system's Hilbert space. This contrasts with Pauli errors, which are specific unitary operators from the Pauli group applied with certain probabilities. The depolarizing channel generalizes Pauli errors by uniformly mixing all possible error operators, capturing isotropic noise in quantum systems.
Physical Origins of Pauli vs Depolarizing Errors
Pauli errors originate from specific quantum noise processes causing bit-flips, phase-flips, or both, represented by the Pauli matrices X, Z, and Y acting on qubits. Depolarizing errors arise when a qubit undergoes random errors uniformly distributed across all possible Pauli operations, effectively modeling isotropic noise from uncontrolled environmental interactions. The physical origin of Pauli errors is often linked to targeted decoherence mechanisms like amplitude damping or phase damping, while depolarizing errors reflect collective effects of complex, stochastic interactions that depolarize the qubit state.
Impact on Quantum Algorithms
Pauli errors introduce specific bit-flip or phase-flip mistakes in qubits, causing predictable disturbances in quantum algorithms and enabling targeted error correction strategies like stabilizer codes. Depolarizing errors result in a uniform randomization of qubit states, leading to more severe decoherence and reduced fidelity, which significantly degrades algorithm performance across all quantum gates. Understanding the differential impact of these errors is crucial for optimizing fault-tolerant quantum circuits and improving the reliability of quantum computations.
Error Correction Techniques for Pauli and Depolarizing Errors
Pauli errors, characterized by bit-flip, phase-flip, or both, are effectively corrected using stabilizer codes such as the Surface Code and Steane Code, which exploit the group properties of Pauli operators for error detection and correction. Depolarizing errors, which introduce a random Pauli operator with equal probability, require more robust error correction techniques like topological codes and concatenated codes that handle mixed error channels by averaging out noise effects. Quantum error correction frameworks leverage syndrome measurement and fault-tolerant gate constructions to maintain coherence and fidelity, addressing the distinct challenges posed by Pauli and depolarizing noise in quantum processors.
Experimental Detection and Mitigation
Pauli errors manifest as bit-flip, phase-flip, or both on qubits and can be experimentally detected using stabilizer measurements in quantum error correction codes like the surface code. Depolarizing errors, representing uniform noise causing any Pauli error with equal probability, are identified through randomized benchmarking protocols that measure the average fidelity decay of quantum gates. Mitigation techniques involve tailored error correction schemes: Pauli errors are corrected by syndrome extraction and decoding algorithms, whereas depolarizing errors require improved hardware calibration and noise-tailored quantum error correction codes to minimize their impact on computation fidelity.
Summary: Comparing Pauli and Depolarizing Errors
Pauli errors represent specific quantum bit-flip, phase-flip, or combined errors characterized by the Pauli operators X, Y, and Z, while depolarizing errors describe a generalized noise model where qubits randomly transition to any error state with equal probability. Pauli errors are often used due to their simplicity and direct correspondence to error syndromes in quantum error correction codes, whereas depolarizing errors provide a more comprehensive and isotropic model of noise affecting all possible error channels. In quantum computing, understanding the distinction helps optimize fault-tolerant strategies by targeting error types precisely or addressing average error effects in noisy intermediate-scale quantum (NISQ) devices.
Pauli Error vs Depolarizing Error Infographic
 techiny.com
techiny.com