Depolarizing noise randomly alters the state of a qubit by applying any of the Pauli errors with equal probability, leading to a complete loss of quantum information over time. Dephasing noise, in contrast, only affects the phase coherences between quantum states without disturbing the populations, causing a decay of off-diagonal elements in the density matrix. Understanding the distinct impacts of depolarizing and dephasing noise is critical for developing error correction techniques and improving quantum coherence in computing systems.
Table of Comparison
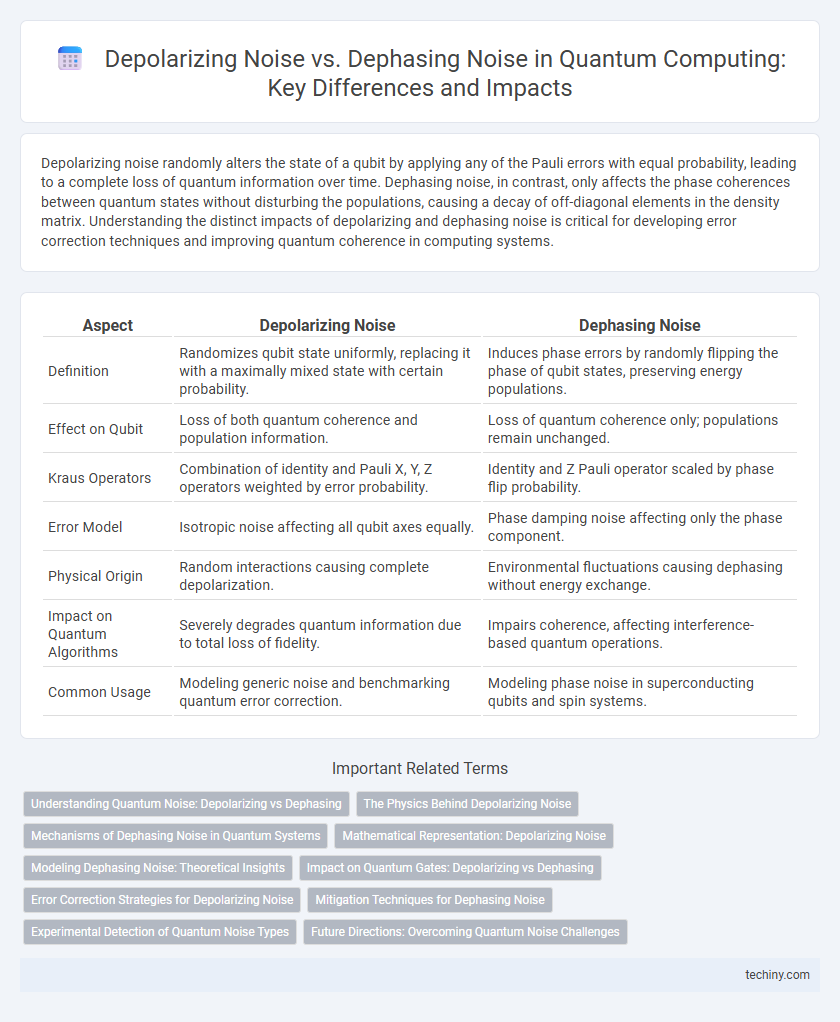
| Aspect | Depolarizing Noise | Dephasing Noise |
|---|---|---|
| Definition | Randomizes qubit state uniformly, replacing it with a maximally mixed state with certain probability. | Induces phase errors by randomly flipping the phase of qubit states, preserving energy populations. |
| Effect on Qubit | Loss of both quantum coherence and population information. | Loss of quantum coherence only; populations remain unchanged. |
| Kraus Operators | Combination of identity and Pauli X, Y, Z operators weighted by error probability. | Identity and Z Pauli operator scaled by phase flip probability. |
| Error Model | Isotropic noise affecting all qubit axes equally. | Phase damping noise affecting only the phase component. |
| Physical Origin | Random interactions causing complete depolarization. | Environmental fluctuations causing dephasing without energy exchange. |
| Impact on Quantum Algorithms | Severely degrades quantum information due to total loss of fidelity. | Impairs coherence, affecting interference-based quantum operations. |
| Common Usage | Modeling generic noise and benchmarking quantum error correction. | Modeling phase noise in superconducting qubits and spin systems. |
Understanding Quantum Noise: Depolarizing vs Dephasing
Depolarizing noise randomly alters the quantum state by applying all possible errors with equal probability, causing a complete loss of quantum information and driving the state towards a maximally mixed state. Dephasing noise specifically affects the coherence between quantum states by disturbing the relative phase, leading to a loss of quantum superposition without energy relaxation. Understanding these distinct noise models is critical for developing effective quantum error correction and noise mitigation strategies in quantum computing.
The Physics Behind Depolarizing Noise
Depolarizing noise arises from random quantum state flips caused by interactions with an uncontrollable environment, leading to a complete loss of quantum information and coherence. This noise model assumes that with a certain probability, the qubit's state is replaced by the maximally mixed state, effectively erasing all encoded information. The physical origin of depolarizing noise can be traced to isotropic errors in qubit operations or uncontrolled couplings with surrounding thermal baths, which equally affect all Pauli directions (X, Y, Z).
Mechanisms of Dephasing Noise in Quantum Systems
Dephasing noise in quantum systems primarily arises from fluctuations in the environment that cause random phase shifts in qubits, leading to loss of coherence without energy exchange. This noise mechanism disrupts the relative phase between quantum states by coupling qubits to low-frequency noise sources such as magnetic field variations and charge fluctuations. Unlike depolarizing noise, which induces random errors uniformly in all bases, dephasing noise selectively affects quantum phase, making it a critical factor in decoherence during quantum information processing.
Mathematical Representation: Depolarizing Noise
Depolarizing noise in quantum computing is mathematically represented by a quantum channel that replaces the quantum state r with a maximally mixed state I/d with probability p, expressed as \( \mathcal{E}(\rho) = (1-p)\rho + \frac{p}{d}I \), where d is the dimension of the Hilbert space. This noise model isotropically shrinks the Bloch sphere, affecting all quantum states uniformly and reducing coherence. Depolarizing noise is often contrasted with dephasing noise, which selectively affects off-diagonal terms in the density matrix without altering population probabilities.
Modeling Dephasing Noise: Theoretical Insights
Dephasing noise in quantum computing is modeled as a process that primarily affects the phase coherence of qubits without altering their energy states, typically represented by a phase-damping channel in quantum operations. This noise model captures the loss of quantum information due to environmental interactions causing random phase fluctuations, which is mathematically characterized by the decay of off-diagonal elements in the qubit's density matrix. Theoretical insights into dephasing noise emphasize its impact on decoherence times and the importance of error correction schemes tailored to mitigate phase errors, contrasting with depolarizing noise that induces symmetric errors across all qubit states.
Impact on Quantum Gates: Depolarizing vs Dephasing
Depolarizing noise uniformly randomizes qubit states, causing errors that affect all quantum gate operations by reducing overall fidelity and increasing gate error rates. Dephasing noise selectively disrupts the phase coherence between quantum states, predominantly degrading gates sensitive to phase information such as controlled-phase or Hadamard gates. Understanding the distinct impact of depolarizing versus dephasing noise is crucial for optimizing error mitigation strategies and improving the reliability of quantum gate implementations.
Error Correction Strategies for Depolarizing Noise
Depolarizing noise affects all qubit states uniformly, causing random flips or phase errors with equal probability, which poses significant challenges for quantum error correction. Error correction strategies for depolarizing noise often rely on stabilizer codes like the surface code and the Shor code, designed to detect and correct both bit-flip and phase-flip errors simultaneously. These codes leverage syndrome measurement to identify error patterns without collapsing quantum information, enabling robust error mitigation in quantum processors subject to depolarizing noise.
Mitigation Techniques for Dephasing Noise
Mitigation techniques for dephasing noise in quantum computing primarily involve dynamical decoupling sequences, which apply carefully timed control pulses to average out phase errors and prolong qubit coherence times. Quantum error correction codes, such as the surface code, are tailored to detect and correct phase-flip errors resulting from dephasing noise. Noise-adaptive gate design and real-time feedback control further enhance robustness against dephasing by continuously calibrating quantum operations to minimize phase disturbances.
Experimental Detection of Quantum Noise Types
Depolarizing noise randomly alters the quantum state across all basis vectors, whereas dephasing noise selectively disrupts the phase coherence without changing populations. Experimental detection leverages quantum process tomography and randomized benchmarking to distinguish these noise channels by analyzing error rates and coherence decay patterns. Precise characterization enables optimized error correction strategies tailored to the dominant noise type in quantum computing systems.
Future Directions: Overcoming Quantum Noise Challenges
Future research in quantum computing aims to develop advanced error correction codes tailored specifically for depolarizing noise and dephasing noise to enhance qubit coherence times. Improvements in hardware design, such as noise-resilient qubit architectures and dynamic decoupling techniques, target the reduction of environmental interactions causing these noise types. Integration of machine learning algorithms for real-time noise characterization and adaptive error mitigation promises significant progress in overcoming quantum noise challenges.
depolarizing noise vs dephasing noise Infographic
 techiny.com
techiny.com