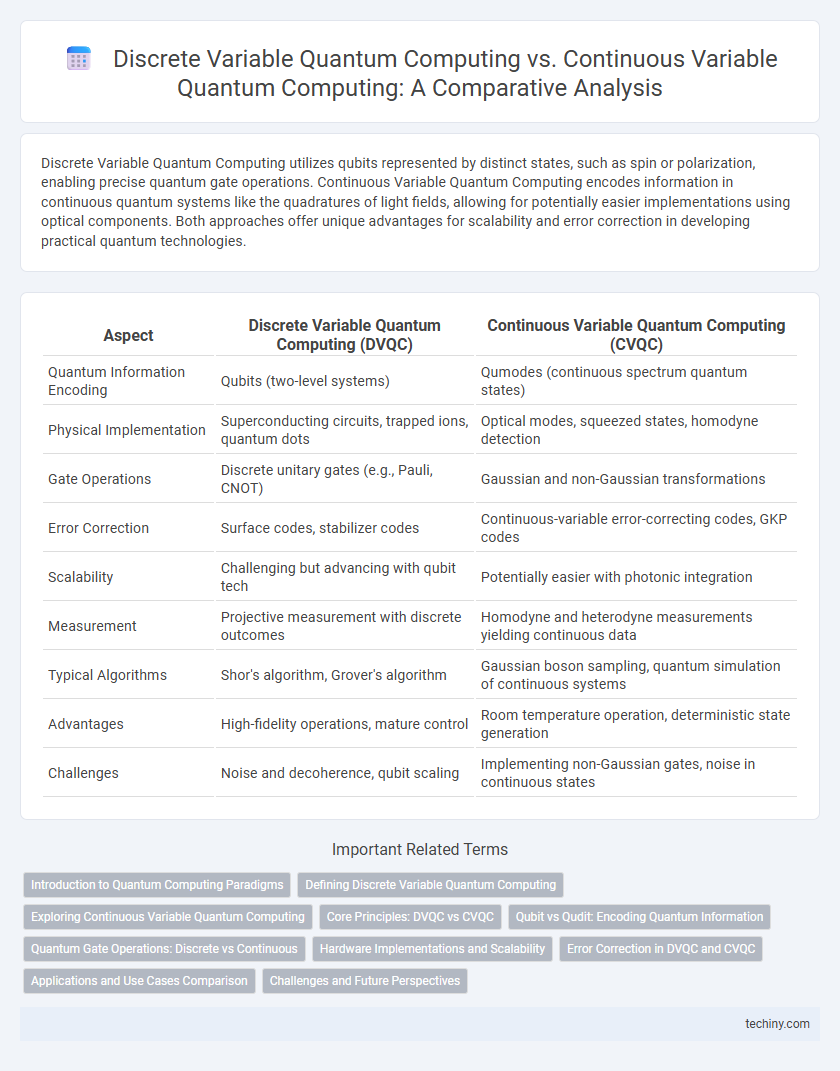
Discrete Variable Quantum Computing utilizes qubits represented by distinct states, such as spin or polarization, enabling precise quantum gate operations. Continuous Variable Quantum Computing encodes information in continuous quantum systems like the quadratures of light fields, allowing for potentially easier implementations using optical components. Both approaches offer unique advantages for scalability and error correction in developing practical quantum technologies.
Table of Comparison
| Aspect | Discrete Variable Quantum Computing (DVQC) | Continuous Variable Quantum Computing (CVQC) |
|---|---|---|
| Quantum Information Encoding | Qubits (two-level systems) | Qumodes (continuous spectrum quantum states) |
| Physical Implementation | Superconducting circuits, trapped ions, quantum dots | Optical modes, squeezed states, homodyne detection |
| Gate Operations | Discrete unitary gates (e.g., Pauli, CNOT) | Gaussian and non-Gaussian transformations |
| Error Correction | Surface codes, stabilizer codes | Continuous-variable error-correcting codes, GKP codes |
| Scalability | Challenging but advancing with qubit tech | Potentially easier with photonic integration |
| Measurement | Projective measurement with discrete outcomes | Homodyne and heterodyne measurements yielding continuous data |
| Typical Algorithms | Shor's algorithm, Grover's algorithm | Gaussian boson sampling, quantum simulation of continuous systems |
| Advantages | High-fidelity operations, mature control | Room temperature operation, deterministic state generation |
| Challenges | Noise and decoherence, qubit scaling | Implementing non-Gaussian gates, noise in continuous states |
Introduction to Quantum Computing Paradigms
Discrete Variable Quantum Computing (DVQC) encodes information in quantum bits (qubits) that exist in distinct states such as |0> and |1> , enabling gate-based quantum algorithms and error-correcting codes. Continuous Variable Quantum Computing (CVQC) manipulates quantum information using continuous spectra of quantum states, typically in quantum optical systems with quadratures of light fields. These paradigms differ fundamentally in physical implementation, noise resilience, and scalability, shaping diverse approaches to quantum algorithm design and hardware development.
Defining Discrete Variable Quantum Computing
Discrete Variable Quantum Computing (DVQC) encodes quantum information using discrete states, typically represented by qubits, which can exist in states |0> or |1> or their superpositions. DVQC relies on quantum gates operating on individual qubits and leverages well-developed quantum circuit models to implement complex algorithms like Shor's and Grover's. This approach contrasts with Continuous Variable Quantum Computing, which manipulates quantum information encoded in continuous spectra such as quadratures of light fields.
Exploring Continuous Variable Quantum Computing
Continuous Variable Quantum Computing leverages quantum states with infinite-dimensional Hilbert spaces, such as the quadratures of light modes, enabling efficient encoding of quantum information through Gaussian states and operations. Unlike Discrete Variable Quantum Computing, which relies on qubits and discrete quantum gates, Continuous Variable systems utilize squeezed states, homodyne detection, and cluster-state methods to achieve fault-tolerant quantum computations. This approach offers advantages in scalability and integration with existing optical technologies, making it a promising candidate for practical quantum computing implementations.
Core Principles: DVQC vs CVQC
Discrete Variable Quantum Computing (DVQC) relies on qubits represented by two-level quantum systems such as spin-1/2 particles or photon polarization states, leveraging quantum gates that manipulate these binary states for computational tasks. Continuous Variable Quantum Computing (CVQC) utilizes quantum information encoded in infinite-dimensional systems like the quadratures of the electromagnetic field, employing continuous quantum variables and Gaussian operations for processing. The core distinction lies in state representation and manipulation, where DVQC uses discrete basis states with unitary gates, while CVQC operates on continuous spectra with transformations often described by symplectic geometry.
Qubit vs Qudit: Encoding Quantum Information
Qubit-based discrete variable quantum computing encodes quantum information in two-level systems, enabling straightforward manipulation and measurement using established quantum gates. In contrast, qudit-based continuous variable quantum computing leverages multilevel systems or continuous spectra, offering higher information density per carrier and potentially enhanced error resilience. The choice between qubit and qudit encoding directly impacts computational complexity, quantum error correction strategies, and scalability of quantum processors.
Quantum Gate Operations: Discrete vs Continuous
Discrete Variable Quantum Computing relies on quantum gate operations that manipulate qubits through a finite set of unitary transformations, typically implemented using discrete quantum logic gates like Pauli-X, Hadamard, and CNOT. Continuous Variable Quantum Computing employs quantum gates acting on continuous-spectrum observables such as position and momentum, utilizing operations like squeezing, displacement, and rotation in phase space. The distinction in quantum gate operations influences error correction schemes and hardware platforms, with discrete gates favoring superconducting qubits and continuous gates aligning with photonic systems.
Hardware Implementations and Scalability
Discrete variable quantum computing relies on qubits realized through superconducting circuits, trapped ions, or spin systems, offering high-fidelity gates but facing challenges in scaling due to error rates and qubit connectivity. Continuous variable quantum computing utilizes optical modes and squeezed states with hardware based on photonic circuits, enabling easier room-temperature operations and potentially larger-scale integration through integrated photonics. Scalability in discrete variable systems is constrained by cryogenic requirements and control complexity, whereas continuous variable platforms benefit from mature optical technology but require advancements in error correction for fault-tolerant large-scale implementations.
Error Correction in DVQC and CVQC
Discrete Variable Quantum Computing (DVQC) utilizes qubits with binary states, relying on well-developed error correction codes like the surface code to mitigate decoherence and gate errors. Continuous Variable Quantum Computing (CVQC) encodes information in quantum states with continuous spectra, requiring bosonic codes such as the Gottesman-Kitaev-Preskill (GKP) code to correct errors stemming from noise in quadratures. Error correction in DVQC is more mature with threshold theorems ensuring fault tolerance, whereas CVQC faces challenges due to infinite-dimensional Hilbert spaces but offers advantages in hardware efficiency and noise resilience through specialized encoding schemes.
Applications and Use Cases Comparison
Discrete Variable Quantum Computing (DVQC) excels in error correction and is widely applied in cryptography and quantum algorithms requiring high fidelity qubit manipulation. Continuous Variable Quantum Computing (CVQC) is advantageous in quantum communication, sensing, and simulations involving harmonic oscillators or Gaussian states, offering scalability with photonic implementations. DVQC suits gate-based quantum computing tasks, while CVQC is preferred for quantum machine learning and real-time quantum signal processing.
Challenges and Future Perspectives
Discrete Variable Quantum Computing faces challenges such as qubit decoherence, scalability limitations, and error correction complexity, which hinder the development of large-scale quantum processors. Continuous Variable Quantum Computing offers advantages in encoding information with infinite-dimensional states but struggles with noise sensitivity and the difficulty of implementing fault-tolerant operations. Future perspectives include hybrid architectures that integrate discrete and continuous variables to leverage robustness and scalability, alongside advancements in quantum error correction techniques and hardware improvements for practical, scalable quantum computing solutions.
Discrete Variable Quantum Computing vs Continuous Variable Quantum Computing Infographic
 techiny.com
techiny.com