In quantum computing, bras and kets are fundamental notations representing quantum states; kets, written as |ps> , denote column vectors in a complex Hilbert space, while bras, written as
Table of Comparison
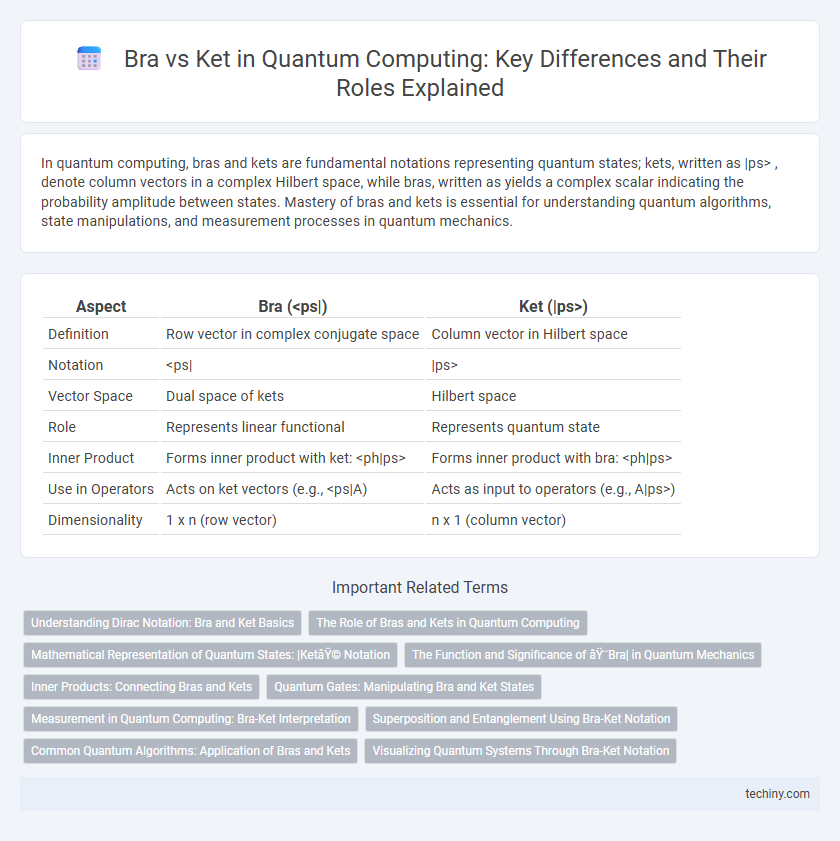
| Aspect | Bra (<ps|) | Ket (|ps>) |
|---|---|---|
| Definition | Row vector in complex conjugate space | Column vector in Hilbert space |
| Notation | <ps| | |ps> |
| Vector Space | Dual space of kets | Hilbert space |
| Role | Represents linear functional | Represents quantum state |
| Inner Product | Forms inner product with ket: <ph|ps> | Forms inner product with bra: <ph|ps> |
| Use in Operators | Acts on ket vectors (e.g., <ps|A) | Acts as input to operators (e.g., A|ps>) |
| Dimensionality | 1 x n (row vector) | n x 1 (column vector) |
Understanding Dirac Notation: Bra and Ket Basics
Dirac notation uses bras
The Role of Bras and Kets in Quantum Computing
Bras and kets are fundamental components of Dirac notation, essential for representing quantum states and their transformations in quantum computing. Kets |ps> denote state vectors in a Hilbert space, while bras The |Ket> notation in quantum computing represents a vector in a complex Hilbert space, fundamental for encoding quantum states. This Dirac notation, introduced by Paul Dirac, provides a concise mathematical framework to describe the state of qubits and facilitates operations such as inner products and outer products. The ket vector |ps> serves as the primary representation for quantum information processing algorithms and quantum gate transformations. The Inner products form the mathematical bridge connecting bras and kets, representing the probability amplitude between quantum states in a Hilbert space. The inner product Quantum gates manipulate bra and ket states by applying unitary transformations to ket vectors, altering their amplitudes and phases within a Hilbert space. Bra vectors represent the complex conjugate transpose of ket states and are essential in calculating probabilities through inner products after gate operations. Common quantum gates like the Hadamard, Pauli-X, and CNOT execute specific changes on ket states, enabling superposition, entanglement, and quantum interference critical for quantum algorithms. Measurement in quantum computing is fundamentally described by the bra-ket notation, where kets |ps> represent quantum states and bras Bra-ket notation, introduced by Paul Dirac, succinctly represents quantum states as kets |ps> and dual vectors as bras Bras and kets form the foundation of Dirac notation used in quantum computing algorithms such as Grover's search and Shor's factoring. Kets represent quantum states in Hilbert space, while bras are their dual vectors facilitating inner product calculations crucial for amplitude measurements. These vectors enable precise manipulation and measurement of quantum states, optimizing algorithm performance and error correction in practical implementations. Bra-ket notation, introduced by physicist Paul Dirac, provides a compact and intuitive way to represent quantum states, where "ket" |ps> denotes a column vector and "bra" Mathematical Representation of Quantum States: |Ket⟩ Notation
The Function and Significance of ⟨Bra| in Quantum Mechanics
Inner Products: Connecting Bras and Kets
Quantum Gates: Manipulating Bra and Ket States
Measurement in Quantum Computing: Bra-Ket Interpretation
Superposition and Entanglement Using Bra-Ket Notation
Common Quantum Algorithms: Application of Bras and Kets
Visualizing Quantum Systems Through Bra-Ket Notation
bra vs ket Infographic
 techiny.com
techiny.com