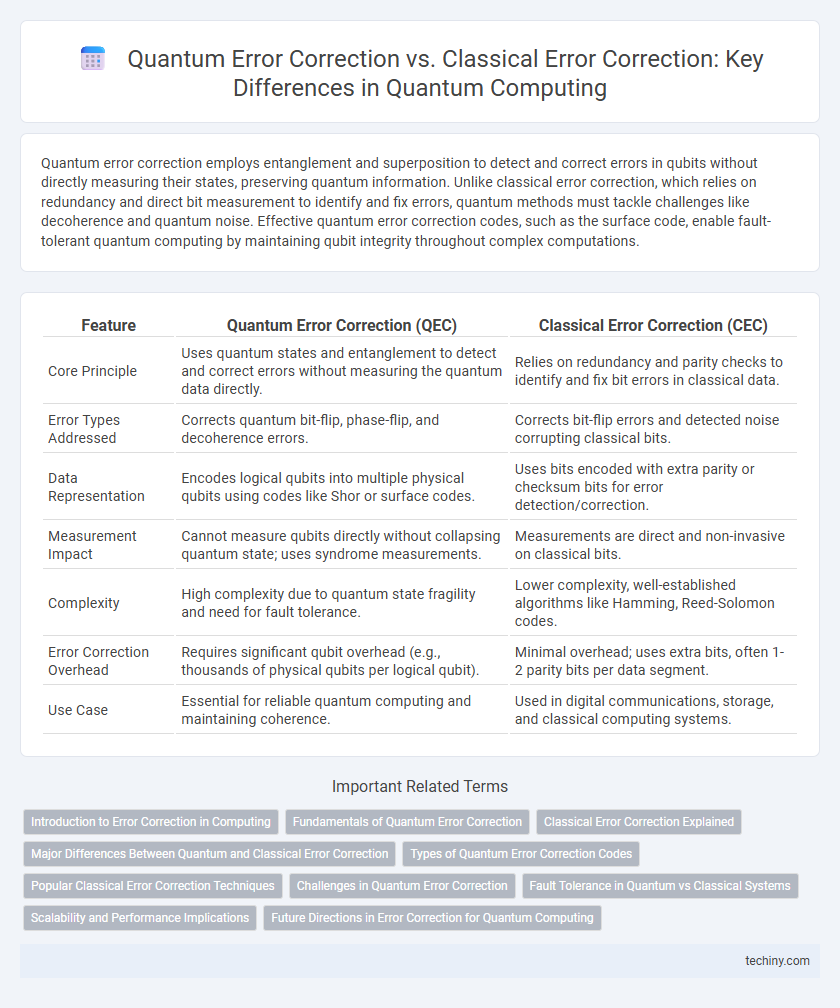
Quantum error correction employs entanglement and superposition to detect and correct errors in qubits without directly measuring their states, preserving quantum information. Unlike classical error correction, which relies on redundancy and direct bit measurement to identify and fix errors, quantum methods must tackle challenges like decoherence and quantum noise. Effective quantum error correction codes, such as the surface code, enable fault-tolerant quantum computing by maintaining qubit integrity throughout complex computations.
Table of Comparison
| Feature | Quantum Error Correction (QEC) | Classical Error Correction (CEC) |
|---|---|---|
| Core Principle | Uses quantum states and entanglement to detect and correct errors without measuring the quantum data directly. | Relies on redundancy and parity checks to identify and fix bit errors in classical data. |
| Error Types Addressed | Corrects quantum bit-flip, phase-flip, and decoherence errors. | Corrects bit-flip errors and detected noise corrupting classical bits. |
| Data Representation | Encodes logical qubits into multiple physical qubits using codes like Shor or surface codes. | Uses bits encoded with extra parity or checksum bits for error detection/correction. |
| Measurement Impact | Cannot measure qubits directly without collapsing quantum state; uses syndrome measurements. | Measurements are direct and non-invasive on classical bits. |
| Complexity | High complexity due to quantum state fragility and need for fault tolerance. | Lower complexity, well-established algorithms like Hamming, Reed-Solomon codes. |
| Error Correction Overhead | Requires significant qubit overhead (e.g., thousands of physical qubits per logical qubit). | Minimal overhead; uses extra bits, often 1-2 parity bits per data segment. |
| Use Case | Essential for reliable quantum computing and maintaining coherence. | Used in digital communications, storage, and classical computing systems. |
Introduction to Error Correction in Computing
Quantum error correction employs qubits and exploits quantum superposition and entanglement to detect and correct errors, addressing issues like decoherence and quantum noise that classical methods cannot handle. Classical error correction relies on redundancy through bits, using techniques such as parity checks and Hamming codes to identify and fix binary errors. The fundamental difference lies in the complex quantum state preservation versus straightforward bit error detection, necessitating specialized quantum algorithms for reliable quantum computation.
Fundamentals of Quantum Error Correction
Quantum error correction fundamentally differs from classical error correction by addressing the unique challenges of quantum information, such as superposition and entanglement, which cannot be duplicated or measured directly without collapsing the quantum state. It employs quantum error-correcting codes like the Shor code or surface codes that protect qubits against decoherence and operational errors through syndrome measurements and recovery operations without destroying quantum data. These codes enable fault-tolerant quantum computation by correcting bit-flip, phase-flip, and combined errors, ensuring the stability of quantum information in noisy quantum environments.
Classical Error Correction Explained
Classical error correction relies on redundancy techniques such as parity bits, Hamming codes, and cyclic redundancy checks to detect and correct bit-flip errors in digital systems. These methods function effectively in classical computing by encoding data with extra bits that facilitate error detection and correction without altering the original information. Unlike quantum error correction, which must address quantum decoherence and superposition errors, classical error correction primarily targets straightforward binary bit errors caused by noise and hardware faults.
Major Differences Between Quantum and Classical Error Correction
Quantum error correction fundamentally differs from classical error correction by addressing errors that involve quantum superposition and entanglement rather than simple bit flips or erasures. Unlike classical error correction codes that deal with discrete binary states, quantum codes must correct both bit-flip and phase-flip errors without directly measuring the quantum state, preserving coherence. The use of quantum redundancy through entangled qubits and syndrome measurement without collapsing the quantum information highlights the intricate complexity unique to quantum error correction schemes.
Types of Quantum Error Correction Codes
Quantum error correction codes, such as Shor, Steane, and surface codes, are designed to protect qubits against decoherence and quantum noise, addressing errors like bit-flip and phase-flip simultaneously. Unlike classical error correction, which primarily handles bit-flip errors through redundancy and parity checks, quantum codes exploit entanglement and superposition to detect and correct errors without measuring the quantum state directly. Topological codes like surface codes offer high fault tolerance and scalability, making them pivotal for practical quantum computing implementations.
Popular Classical Error Correction Techniques
Popular classical error correction techniques include Hamming codes, Reed-Solomon codes, and Turbo codes, which efficiently detect and correct bit-flip errors in digital communication and storage systems. These methods rely on redundancy and parity checks to identify erroneous bits and restore original data with high reliability. Unlike quantum error correction, classical techniques do not address quantum decoherence or superposition errors, which require more complex qubit-specific protocols.
Challenges in Quantum Error Correction
Quantum error correction faces unique challenges compared to classical error correction due to the fragile nature of quantum states and the no-cloning theorem, which prevents copying quantum information. Quantum errors are continuous and involve both amplitude and phase, requiring complex encoding schemes like surface codes and stabilizer codes to detect and correct errors without directly measuring qubits. The high error rates and limited qubit coherence times demand significant overhead in qubit resources and sophisticated fault-tolerant protocols to achieve reliable quantum computation.
Fault Tolerance in Quantum vs Classical Systems
Quantum error correction employs entanglement and superposition to detect and correct errors without directly measuring qubits, enabling fault tolerance despite fragile quantum states. Classical error correction relies on redundancy and parity checks to identify and fix bit flips, achieving fault tolerance in digital communication and storage systems. Fault tolerance in quantum systems demands more complex protocols, such as surface codes and topological codes, to protect against decoherence, while classical systems use well-established coding methods like Hamming or Reed-Solomon codes.
Scalability and Performance Implications
Quantum error correction employs entanglement and superposition to detect and correct qubit errors, requiring exponentially more resources than classical error correction codes for scalability. Unlike classical codes that efficiently handle bit-flip and phase-flip errors with linear redundancy, quantum codes face performance challenges due to decoherence and error propagation across entangled states. The resource overhead and fault-tolerant thresholds significantly impact the scalability of quantum systems, necessitating advanced syndrome measurement techniques and hardware improvements to approach reliable large-scale quantum computing.
Future Directions in Error Correction for Quantum Computing
Quantum error correction for quantum computing demands highly sophisticated protocols due to qubit fragility and quantum decoherence, contrasting with classical error correction methods that rely on simple redundancy and parity checks. Future directions emphasize developing fault-tolerant quantum codes like surface codes and concatenated codes to enable scalable, reliable quantum processors. Advances in machine learning algorithms and hardware improvements aim to optimize error syndrome detection, reduce overhead, and accelerate real-time error correction in quantum systems.
Quantum Error Correction vs Classical Error Correction Infographic
 techiny.com
techiny.com