Boson sampling leverages the quantum properties of identical bosons to solve specific sampling problems that are intractable for classical computers, making it a powerful but specialized quantum simulation technique. Universal quantum computation, in contrast, utilizes a broad set of quantum gates to perform any computational task, offering greater versatility and the potential to implement complex algorithms like Shor's or Grover's. While boson sampling demonstrates quantum advantage in restricted scenarios, universal quantum computers aim to achieve wider applicability across diverse problems in cryptography, optimization, and machine learning.
Table of Comparison
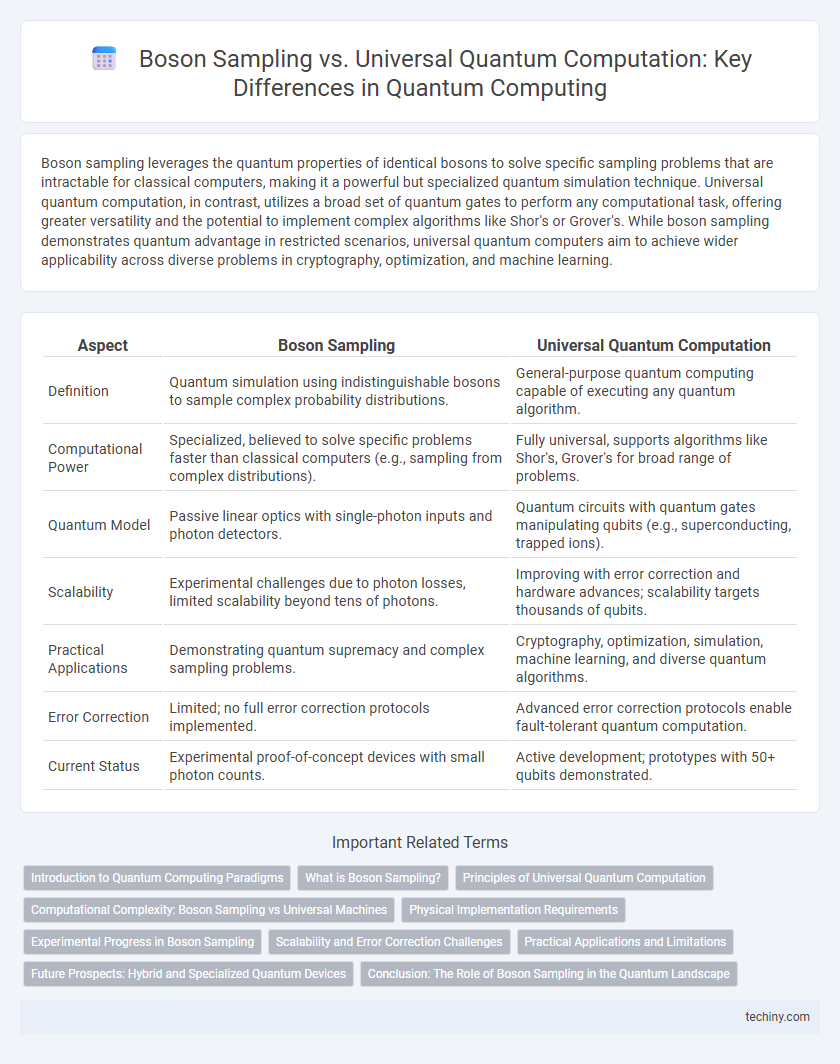
| Aspect | Boson Sampling | Universal Quantum Computation |
|---|---|---|
| Definition | Quantum simulation using indistinguishable bosons to sample complex probability distributions. | General-purpose quantum computing capable of executing any quantum algorithm. |
| Computational Power | Specialized, believed to solve specific problems faster than classical computers (e.g., sampling from complex distributions). | Fully universal, supports algorithms like Shor's, Grover's for broad range of problems. |
| Quantum Model | Passive linear optics with single-photon inputs and photon detectors. | Quantum circuits with quantum gates manipulating qubits (e.g., superconducting, trapped ions). |
| Scalability | Experimental challenges due to photon losses, limited scalability beyond tens of photons. | Improving with error correction and hardware advances; scalability targets thousands of qubits. |
| Practical Applications | Demonstrating quantum supremacy and complex sampling problems. | Cryptography, optimization, simulation, machine learning, and diverse quantum algorithms. |
| Error Correction | Limited; no full error correction protocols implemented. | Advanced error correction protocols enable fault-tolerant quantum computation. |
| Current Status | Experimental proof-of-concept devices with small photon counts. | Active development; prototypes with 50+ qubits demonstrated. |
Introduction to Quantum Computing Paradigms
Boson Sampling leverages the computational complexity of simulating bosons passing through a linear optical network, offering a specialized approach within quantum computing paradigms. Universal Quantum Computation, in contrast, encompasses a broader framework with the ability to perform any quantum algorithm via a universal set of quantum gates. Understanding these paradigms highlights the distinction between problem-specific quantum advantage in Boson Sampling and the general-purpose capabilities of Universal Quantum Computers.
What is Boson Sampling?
Boson Sampling is a specialized quantum computational task that involves sampling from the probability distribution of indistinguishable bosons, such as photons, passing through a linear optical network. Unlike universal quantum computation, which can perform a wide range of algorithms, Boson Sampling is designed for a narrow problem that is believed to be hard for classical computers to efficiently simulate. This approach leverages the quantum interference of bosons but does not support universal quantum gate operations, making it a near-term demonstration of quantum advantage through photonic systems.
Principles of Universal Quantum Computation
Universal quantum computation relies on the manipulation of qubits through a set of universal gates that enable the execution of any quantum algorithm, incorporating operations such as entanglement and superposition. This model contrasts with boson sampling, which uses non-universal linear optical networks to sample output distributions of indistinguishable bosons, primarily for demonstrating quantum advantage. The principles of universal quantum computation emphasize fault tolerance, error correction, and programmability, facilitating scalable quantum processing beyond specialized tasks like boson sampling.
Computational Complexity: Boson Sampling vs Universal Machines
Boson Sampling leverages the complexity of calculating matrix permanents, a #P-hard problem, making it computationally infeasible for classical algorithms to simulate efficiently, unlike universal quantum computers designed for general-purpose quantum algorithms. Universal quantum computation encompasses a broader class of problems, utilizing gate-based models to achieve BQP-complete complexity, thus enabling polynomial-time solutions to many problems believed intractable classically. The restricted model of Boson Sampling, while not universal, provides strong evidence of quantum supremacy through specialized quantum tasks beyond classical reach but lacks the algorithmic versatility of universal quantum machines.
Physical Implementation Requirements
Boson sampling requires specialized photonic systems with highly indistinguishable single photons and low-loss linear optical networks, emphasizing scalable multiplexed photon sources and time-bin encoding. Universal quantum computation demands more complex physical platforms like superconducting qubits or trapped ions with high-fidelity gate operations, quantum error correction, and qubit connectivity. The boson sampling model simplifies experimental setups by avoiding full error correction but sacrifices computational universality compared to universal quantum computers.
Experimental Progress in Boson Sampling
Experimental progress in Boson Sampling has demonstrated scalable photonic setups capable of generating multiple indistinguishable photons, advancing verification techniques and error mitigation strategies. Integrated photonic chips and superconducting detectors have improved photon generation rates and detection efficiency, enhancing the feasibility of Boson Sampling as a means to demonstrate quantum advantage. These developments contrast with universal quantum computation, which requires error-corrected qubits and complex gate operations, highlighting Boson Sampling's role as a more near-term demonstration of quantum supremacy.
Scalability and Error Correction Challenges
Boson Sampling offers a specialized approach to quantum computation that excels in demonstrating quantum advantage for specific problems but faces significant scalability limitations due to the exponential increase in required photon sources and detectors. Universal Quantum Computation provides a more flexible framework capable of executing any quantum algorithm, yet it encounters substantial challenges in implementing fault-tolerant error correction codes such as the surface code to maintain coherence and reduce noise. Achieving scalable quantum advantage thus demands overcoming these error correction complexities and developing hardware that supports large qubit counts with high fidelity.
Practical Applications and Limitations
Boson Sampling excels in demonstrating quantum supremacy with specific tasks like simulating molecular vibrations and solving linear algebra problems but lacks the versatility of universal quantum computation. Universal quantum computers offer broader practical applications including cryptography, optimization, and complex system simulations, though they face significant challenges in error correction and scalability. Limitations of Boson Sampling include its reliance on photonic systems and limited computational scope, while universal quantum computation struggles with coherence times and fault-tolerant implementation complexity.
Future Prospects: Hybrid and Specialized Quantum Devices
Boson Sampling offers a promising pathway to demonstrate quantum advantage through specialized quantum devices optimized for specific tasks, potentially accelerating problem-solving in fields like cryptography and materials science. Universal quantum computation aims for broad applicability by leveraging qubits and error correction to perform a wide range of algorithms, but it faces scalability and coherence challenges. Future prospects focus on hybrid architectures combining Boson Sampling's efficiency with universal quantum processors, enabling versatile, high-performance quantum systems tailored for both specialized and general-purpose applications.
Conclusion: The Role of Boson Sampling in the Quantum Landscape
Boson sampling serves as a specialized quantum computing model that exploits the complexity of photon interference to demonstrate quantum advantage in sampling tasks. Unlike universal quantum computation, which aims to perform any computational task efficiently, boson sampling is tailored for specific problems believed to be intractable for classical computers. Its role lies in validating quantum supremacy and advancing photonic quantum technologies while highlighting the challenges of scalability and error correction inherent to universal quantum machines.
Boson Sampling vs Universal Quantum Computation Infographic
 techiny.com
techiny.com