Pauli matrices are fundamental in quantum computing for representing quantum gate operations on qubits, characterized by their distinct properties of being Hermitian and unitary with eigenvalues +-1. The identity matrix serves as a neutral element, leaving quantum states unchanged, playing a critical role in constructing more complex operations through tensor products with Pauli matrices. Combining Pauli and identity matrices enables precise manipulation of multi-qubit systems, essential for implementing quantum algorithms and error correction codes.
Table of Comparison
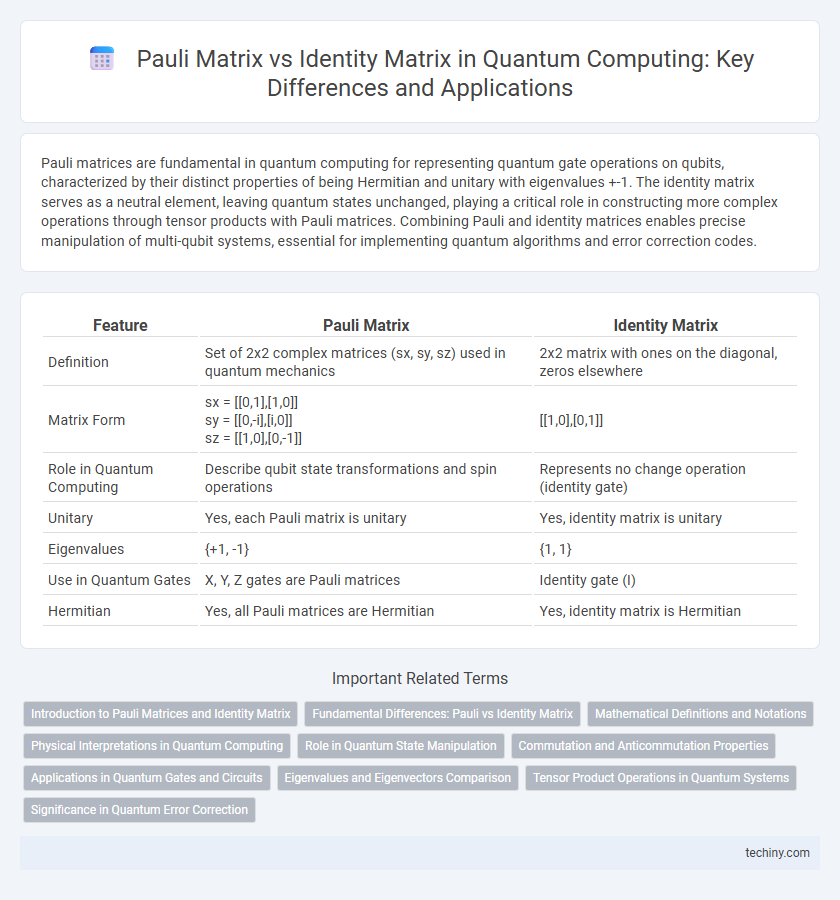
| Feature | Pauli Matrix | Identity Matrix |
|---|---|---|
| Definition | Set of 2x2 complex matrices (sx, sy, sz) used in quantum mechanics | 2x2 matrix with ones on the diagonal, zeros elsewhere |
| Matrix Form |
sx = [[0,1],[1,0]] sy = [[0,-i],[i,0]] sz = [[1,0],[0,-1]] |
[[1,0],[0,1]] |
| Role in Quantum Computing | Describe qubit state transformations and spin operations | Represents no change operation (identity gate) |
| Unitary | Yes, each Pauli matrix is unitary | Yes, identity matrix is unitary |
| Eigenvalues | {+1, -1} | {1, 1} |
| Use in Quantum Gates | X, Y, Z gates are Pauli matrices | Identity gate (I) |
| Hermitian | Yes, all Pauli matrices are Hermitian | Yes, identity matrix is Hermitian |
Introduction to Pauli Matrices and Identity Matrix
Pauli matrices are a set of three 2x2 complex Hermitian and unitary matrices fundamental in quantum computing for representing quantum spin operators. The identity matrix, a 2x2 matrix with ones on the diagonal and zeros elsewhere, acts as the neutral element in matrix multiplication and is essential for maintaining the state unchanged in quantum operations. Together, Pauli matrices and the identity matrix form a basis for describing single-qubit quantum gates and operators in quantum information processing.
Fundamental Differences: Pauli vs Identity Matrix
Pauli matrices consist of three 2x2 complex Hermitian and unitary matrices representing quantum spin operators, crucial for describing qubit state transformations, whereas the identity matrix serves as the neutral element in quantum operations, preserving states without alteration. Pauli matrices exhibit non-commutative properties enabling quantum gate functionalities like bit-flip and phase-flip, while the identity matrix commutes with all matrices, maintaining state consistency. The fundamental distinction lies in Pauli matrices' role in inducing state changes and encoding quantum information, contrasting with the identity matrix's role as a quantum operator that leaves qubits unchanged.
Mathematical Definitions and Notations
Pauli matrices, denoted as s_x, s_y, and s_z, are 2x2 complex Hermitian and unitary matrices used to represent quantum spin operators in quantum computing. The identity matrix I, a 2x2 matrix with ones on the diagonal and zeros elsewhere, serves as the neutral element in matrix multiplication and leaves quantum states unchanged. Pauli matrices satisfy the commutation and anticommutation relations important for qubit manipulation, while the identity matrix acts as the baseline operator in quantum circuits.
Physical Interpretations in Quantum Computing
Pauli matrices represent quantum spin operators essential for describing qubit state rotations and quantum gate operations, reflecting physical spin measurements along specific axes. The identity matrix symbolizes the no-operation gate, preserving qubit states without alteration, crucial for quantum circuit design and coherence. Together, they form the basis of single-qubit transformations, directly linking mathematical operators to measurable physical phenomena in quantum systems.
Role in Quantum State Manipulation
Pauli matrices serve as fundamental operators in quantum state manipulation, enabling qubit rotations and transformations critical for quantum algorithms. Unlike the identity matrix, which leaves quantum states unchanged, Pauli matrices actively alter the state vector by performing bit-flip (X), phase-flip (Z), and combined bit-phase-flip (Y) operations. These matrices form the basis for constructing quantum gates and are essential in error correction and entanglement protocols within quantum computing.
Commutation and Anticommutation Properties
Pauli matrices \( \sigma_x, \sigma_y, \sigma_z \) exhibit specific anticommutation relations, satisfying \(\{\sigma_i, \sigma_j\} = 2\delta_{ij}I\), where \(I\) is the identity matrix and \(\delta_{ij}\) is the Kronecker delta. The identity matrix \(I\) commutes with all Pauli matrices, fulfilling \([I, \sigma_i] = 0\) for \(i = x,y,z\), reflecting its role as the neutral element in operator algebra. These commutation and anticommutation properties underpin the fundamental algebraic structure used in quantum computing for describing spin operators and quantum gates.
Applications in Quantum Gates and Circuits
Pauli matrices (X, Y, Z) serve as fundamental quantum gates, enabling qubit state rotations and bit-flip or phase-flip operations vital for quantum algorithms and error correction. The identity matrix acts as the no-operation gate, preserving qubit states while allowing synchronization and timing control within quantum circuits. Together, they form the building blocks of complex quantum gate sequences, facilitating universal quantum computation and circuit design.
Eigenvalues and Eigenvectors Comparison
Pauli matrices possess eigenvalues of +-1 and distinct eigenvectors that form an orthonormal basis crucial for quantum state manipulation, whereas the identity matrix has a single eigenvalue of 1 with every vector as an eigenvector, reflecting no change in state. The eigenvectors of Pauli matrices correspond to spin- 1/2 particle states along different axes, enabling quantum gate operations and state rotations. In contrast, the identity matrix maintains all quantum states unchanged, serving as a neutral operator in quantum computations.
Tensor Product Operations in Quantum Systems
The Pauli matrices, fundamental in quantum computing, represent single-qubit quantum operators essential for describing spin and quantum state transformations. The identity matrix acts as a neutral element in tensor product operations, preserving the state of qubits when combined with Pauli matrices. Tensor product operations enable the construction of multi-qubit operators by combining Pauli matrices and identity matrices, facilitating complex quantum gate implementations and entanglement analysis in quantum systems.
Significance in Quantum Error Correction
Pauli matrices, fundamental operators in quantum computing, serve as the primary error models in quantum error correction by representing bit-flip, phase-flip, and combined errors on qubits; their algebraic properties enable efficient detection and correction of such errors within quantum codes. In contrast, the identity matrix acts as the null operation, indicating no error has occurred, and forms the baseline for error syndrome measurements. The interplay between Pauli matrices and the identity matrix underpins the structure of stabilizer codes, which are pivotal for maintaining qubit coherence in noisy quantum environments.
Pauli matrix vs identity matrix Infographic
 techiny.com
techiny.com