Quantum annealing leverages quantum tunneling to explore energy landscapes more efficiently than classical annealing, which relies on thermal fluctuations to escape local minima. Unlike classical annealing, quantum annealing can simultaneously evaluate multiple states, potentially achieving faster convergence on optimal solutions for complex optimization problems. This advantages quantum annealing in scenarios where traditional methods struggle with high-dimensional or rugged energy landscapes.
Table of Comparison
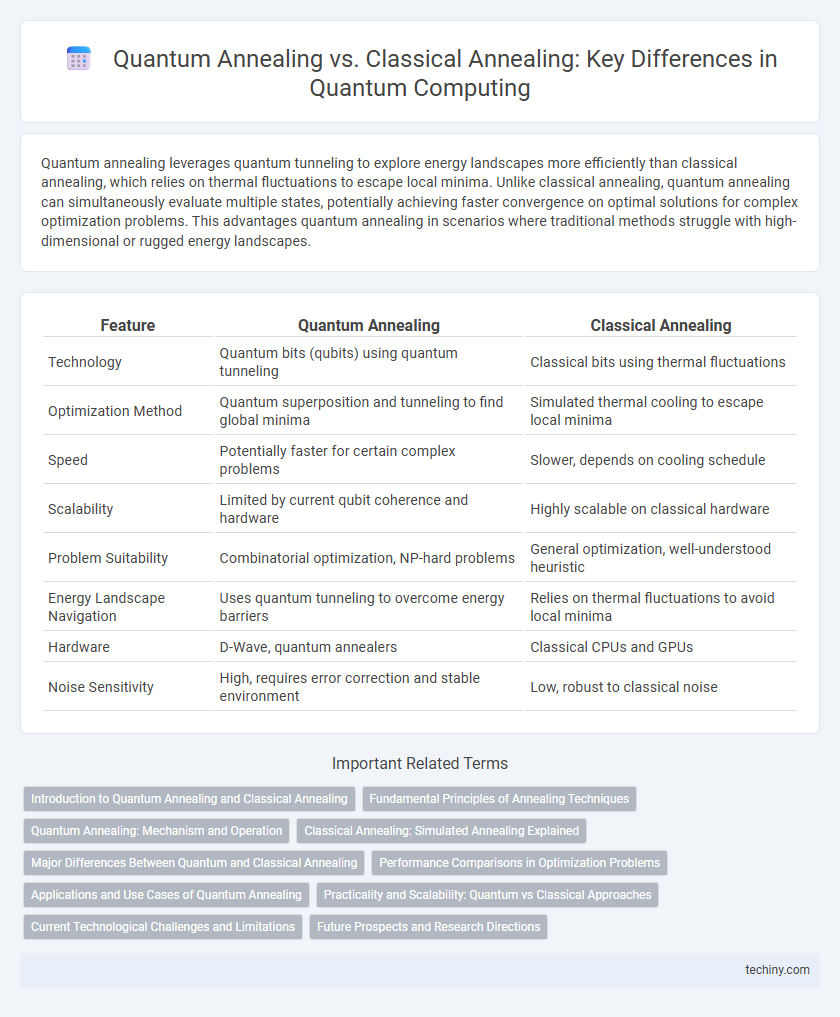
| Feature | Quantum Annealing | Classical Annealing |
|---|---|---|
| Technology | Quantum bits (qubits) using quantum tunneling | Classical bits using thermal fluctuations |
| Optimization Method | Quantum superposition and tunneling to find global minima | Simulated thermal cooling to escape local minima |
| Speed | Potentially faster for certain complex problems | Slower, depends on cooling schedule |
| Scalability | Limited by current qubit coherence and hardware | Highly scalable on classical hardware |
| Problem Suitability | Combinatorial optimization, NP-hard problems | General optimization, well-understood heuristic |
| Energy Landscape Navigation | Uses quantum tunneling to overcome energy barriers | Relies on thermal fluctuations to avoid local minima |
| Hardware | D-Wave, quantum annealers | Classical CPUs and GPUs |
| Noise Sensitivity | High, requires error correction and stable environment | Low, robust to classical noise |
Introduction to Quantum Annealing and Classical Annealing
Quantum annealing leverages quantum tunneling to escape local minima in optimization problems, offering potential speedups over classical annealing, which relies on thermal fluctuations to gradually settle into a global minimum. Classical annealing simulates the cooling process of materials to minimize energy states and solve combinatorial problems, while quantum annealing exploits quantum superposition and entanglement to explore solution spaces more efficiently. Both methods aim at global optimization, but quantum annealing harnesses quantum mechanics principles to potentially outperform classical simulated annealing in specific complex problem scenarios.
Fundamental Principles of Annealing Techniques
Quantum annealing leverages quantum tunneling to explore energy landscapes, enabling the system to bypass high energy barriers and seek global minima more efficiently than classical annealing, which relies on thermal fluctuations to overcome such barriers. Classical annealing employs gradual cooling to reduce thermal energy, allowing the system to settle into lower-energy states by probabilistically escaping local minima. The fundamental difference lies in quantum annealing's utilization of superposition and tunneling effects, contrasting with the purely stochastic thermal processes in classical annealing.
Quantum Annealing: Mechanism and Operation
Quantum annealing leverages quantum tunneling to explore energy landscapes more efficiently than classical annealing, enabling solutions to optimization problems by gradually evolving a quantum system towards its ground state. This process uses superconducting qubits and transverse magnetic fields to induce quantum fluctuations, allowing the system to escape local minima and find global minima more effectively. The quantum annealer operates at ultra-low temperatures to maintain coherence, optimizing problem-solving in fields such as material science and cryptography.
Classical Annealing: Simulated Annealing Explained
Simulated annealing is a probabilistic optimization technique inspired by the annealing process in metallurgy, where controlled cooling allows atoms to reach a minimum energy state. It iteratively explores the solution space by accepting worse solutions with a probability that decreases over time, enabling it to escape local minima and approach global optima. Widely applied in combinatorial optimization, simulated annealing excels in solving problems like the traveling salesman and scheduling by mimicking thermal fluctuations in classical systems.
Major Differences Between Quantum and Classical Annealing
Quantum annealing leverages quantum tunneling to escape local minima more efficiently, enhancing optimization in complex energy landscapes, whereas classical annealing relies on thermal fluctuations to explore solutions. Quantum annealing operates at near absolute zero temperatures to maintain quantum coherence, while classical annealing uses temperature gradients to probabilistically accept changes. The probabilistic nature of state transitions differs fundamentally; quantum annealing exploits superposition and entanglement, unlike the purely stochastic process of classical annealing.
Performance Comparisons in Optimization Problems
Quantum annealing leverages quantum tunneling to escape local minima more efficiently than classical annealing, which relies on thermal fluctuations. Studies demonstrate that quantum annealers outperform classical simulated annealing on certain combinatorial optimization problems, especially those with rugged energy landscapes and large solution spaces. However, classical annealing remains competitive in problems with smoother cost functions or smaller scales due to its lower hardware complexity and broader algorithmic flexibility.
Applications and Use Cases of Quantum Annealing
Quantum annealing excels in solving complex combinatorial optimization problems, such as portfolio optimization in finance, protein folding in bioinformatics, and logistics routing in supply chain management, where classical annealing struggles with scalability. Its ability to explore vast solution spaces through quantum superposition enables more efficient identification of global minima in problems with rugged energy landscapes. This makes quantum annealing particularly valuable for industries requiring rapid and high-quality solutions in scheduling, machine learning model training, and cryptographic analysis.
Practicality and Scalability: Quantum vs Classical Approaches
Quantum annealing leverages quantum tunneling to explore complex optimization landscapes more efficiently than classical annealing, offering potential advantages in solving large-scale problems with rugged energy surfaces. Classical annealing relies on thermal fluctuations to escape local minima, which can be less effective as problem size and complexity increase, impacting its scalability. Quantum annealers, while still limited by qubit coherence and hardware constraints, show promising scalability prospects through advancements in quantum hardware, potentially surpassing classical methods in practical applications involving combinatorial optimization.
Current Technological Challenges and Limitations
Quantum annealing faces significant challenges such as qubit coherence time limitations, error rates, and scalability constraints compared to classical annealing's well-established algorithmic frameworks and hardware reliability. The quantum approach requires maintaining fragile quantum states and overcoming noise interference, which currently limits problem sizes and solution accuracy. In contrast, classical annealing benefits from mature optimization techniques but struggles with combinatorial explosion for complex problems that quantum annealing aims to address.
Future Prospects and Research Directions
Quantum annealing leverages quantum tunneling effects to escape local minima more efficiently than classical annealing, promising accelerated solutions for complex optimization problems in fields like logistics and drug discovery. Emerging research focuses on hybrid quantum-classical algorithms and error mitigation techniques to enhance scalability and practical applicability of quantum annealers. Future prospects include integrating quantum annealing with machine learning frameworks and exploring novel quantum materials to improve coherence times and problem-solving capabilities.
Quantum Annealing vs Classical Annealing Infographic
 techiny.com
techiny.com