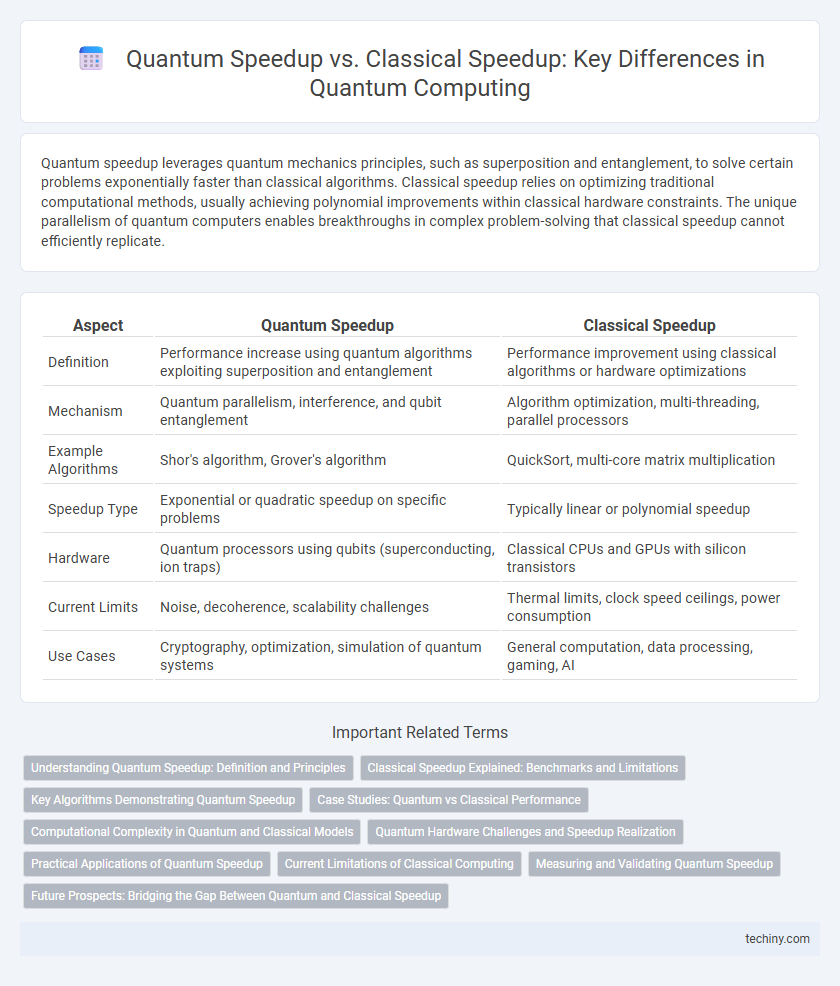
Quantum speedup leverages quantum mechanics principles, such as superposition and entanglement, to solve certain problems exponentially faster than classical algorithms. Classical speedup relies on optimizing traditional computational methods, usually achieving polynomial improvements within classical hardware constraints. The unique parallelism of quantum computers enables breakthroughs in complex problem-solving that classical speedup cannot efficiently replicate.
Table of Comparison
| Aspect | Quantum Speedup | Classical Speedup |
|---|---|---|
| Definition | Performance increase using quantum algorithms exploiting superposition and entanglement | Performance improvement using classical algorithms or hardware optimizations |
| Mechanism | Quantum parallelism, interference, and qubit entanglement | Algorithm optimization, multi-threading, parallel processors |
| Example Algorithms | Shor's algorithm, Grover's algorithm | QuickSort, multi-core matrix multiplication |
| Speedup Type | Exponential or quadratic speedup on specific problems | Typically linear or polynomial speedup |
| Hardware | Quantum processors using qubits (superconducting, ion traps) | Classical CPUs and GPUs with silicon transistors |
| Current Limits | Noise, decoherence, scalability challenges | Thermal limits, clock speed ceilings, power consumption |
| Use Cases | Cryptography, optimization, simulation of quantum systems | General computation, data processing, gaming, AI |
Understanding Quantum Speedup: Definition and Principles
Quantum speedup refers to the advantage quantum algorithms provide by solving problems faster than the best-known classical algorithms, often measured in terms of computational complexity reductions. It is achieved through quantum principles such as superposition, entanglement, and interference, enabling parallelism and problem-space exploration unattainable by classical means. Understanding quantum speedup involves analyzing algorithmic efficiency, problem structure, and the limitations of both quantum and classical approaches in specific computational tasks.
Classical Speedup Explained: Benchmarks and Limitations
Classical speedup refers to performance improvements achieved through optimized algorithms or hardware on traditional computing architectures, measured by benchmarks like FLOPS or execution time reductions on problems such as sorting or matrix multiplication. Despite these gains, classical speedup faces limitations in scaling efficiently for complex tasks like factoring large integers or simulating quantum systems, where exponential resource requirements emerge. Understanding these constraints highlights why quantum speedup, leveraging superposition and entanglement, offers potentially transformative advantages in computational complexity beyond classical capabilities.
Key Algorithms Demonstrating Quantum Speedup
Shor's algorithm exemplifies quantum speedup by efficiently factoring large integers exponentially faster than the best-known classical algorithms, impacting cryptography. Grover's algorithm provides a quadratic speedup for unstructured search problems, improving database search times significantly over classical counterparts. Quantum simulation algorithms enable modeling of quantum systems in polynomial time, a task that becomes intractable for classical computers as system complexity increases.
Case Studies: Quantum vs Classical Performance
Quantum speedup demonstrates significant advantages in specific case studies such as factoring large integers using Shor's algorithm, where quantum processors outperform classical algorithms exponentially. In optimization problems like the Traveling Salesman Problem, quantum annealers have shown promising speedup compared to classical heuristics under certain conditions. Benchmarking quantum hardware against classical supercomputers reveals that quantum devices can solve particular classes of problems with reduced time complexity, though broad applicability remains under research.
Computational Complexity in Quantum and Classical Models
Quantum speedup leverages quantum superposition and entanglement to solve specific problems, such as factoring large integers or simulating quantum systems, exponentially faster than classical algorithms. Computational complexity in quantum models often reduces problems from NP-hard in classical paradigms to BQP, highlighting practical efficiency gains in tasks like unstructured search and optimization. Classical speedup relies on algorithmic improvements and hardware advancements but remains constrained by polynomial or exponential time complexities that quantum algorithms can transcend.
Quantum Hardware Challenges and Speedup Realization
Quantum speedup relies on leveraging quantum phenomena like superposition and entanglement to solve specific problems exponentially faster than classical algorithms. Realizing this advantage depends heavily on overcoming quantum hardware challenges such as qubit coherence times, error rates, and scalability constraints. While classical speedup benefits from well-established architectures, quantum hardware must achieve fault-tolerant qubits and efficient quantum error correction methods to enable true practical speedup.
Practical Applications of Quantum Speedup
Quantum speedup demonstrates significant advantages over classical speedup in complex optimization problems, cryptographic algorithms, and large-scale data analysis. Practical applications include quantum machine learning models that process vast datasets exponentially faster and quantum simulations that enable breakthroughs in drug discovery and materials science. These capabilities surpass classical approaches by exploiting quantum superposition and entanglement, resulting in unprecedented computational efficiency.
Current Limitations of Classical Computing
Classical computing faces limitations such as Moore's Law reaching physical and economic constraints, limiting transistor miniaturization, and increased heat dissipation restricting clock speed improvements. These bottlenecks hinder classical algorithms from efficiently solving certain complex problems like large-scale factorization and optimization. Quantum speedup leverages quantum parallelism and entanglement to surpass these barriers, offering exponential acceleration in specific computational tasks unattainable by classical methods.
Measuring and Validating Quantum Speedup
Measuring quantum speedup involves benchmarking quantum algorithms against the best-known classical algorithms for specific computational problems, with attention to problem size and error rates. Validation requires rigorous statistical analysis and reproducibility of results across different quantum hardware platforms to ensure that observed speedup is not due to noise or hardware-specific artifacts. Quantitative metrics such as time complexity, circuit depth, and fidelity are critical to compare quantum speedup meaningfully against classical methods.
Future Prospects: Bridging the Gap Between Quantum and Classical Speedup
Quantum computing promises exponential speedup for certain complex problems, surpassing classical algorithms limited by polynomial time constraints. Research is actively exploring hybrid quantum-classical frameworks to harness quantum advantages while leveraging classical stability and scalability. Future prospects hinge on optimizing quantum error correction and algorithm design to bridge the performance gap and enable practical, large-scale quantum speedup.
Quantum Speedup vs Classical Speedup Infographic
 techiny.com
techiny.com