Continuous-variable quantum computing leverages quantum states with infinite-dimensional Hilbert spaces, such as the quadratures of electromagnetic fields, enabling more natural implementations of certain algorithms and error correction codes. Discrete-variable quantum computing relies on two-level quantum systems like qubits, which are easier to manipulate with existing quantum gate models but face scalability challenges. The choice between continuous-variable and discrete-variable approaches impacts quantum hardware design, error resilience, and algorithm efficiency in practical quantum computing applications.
Table of Comparison
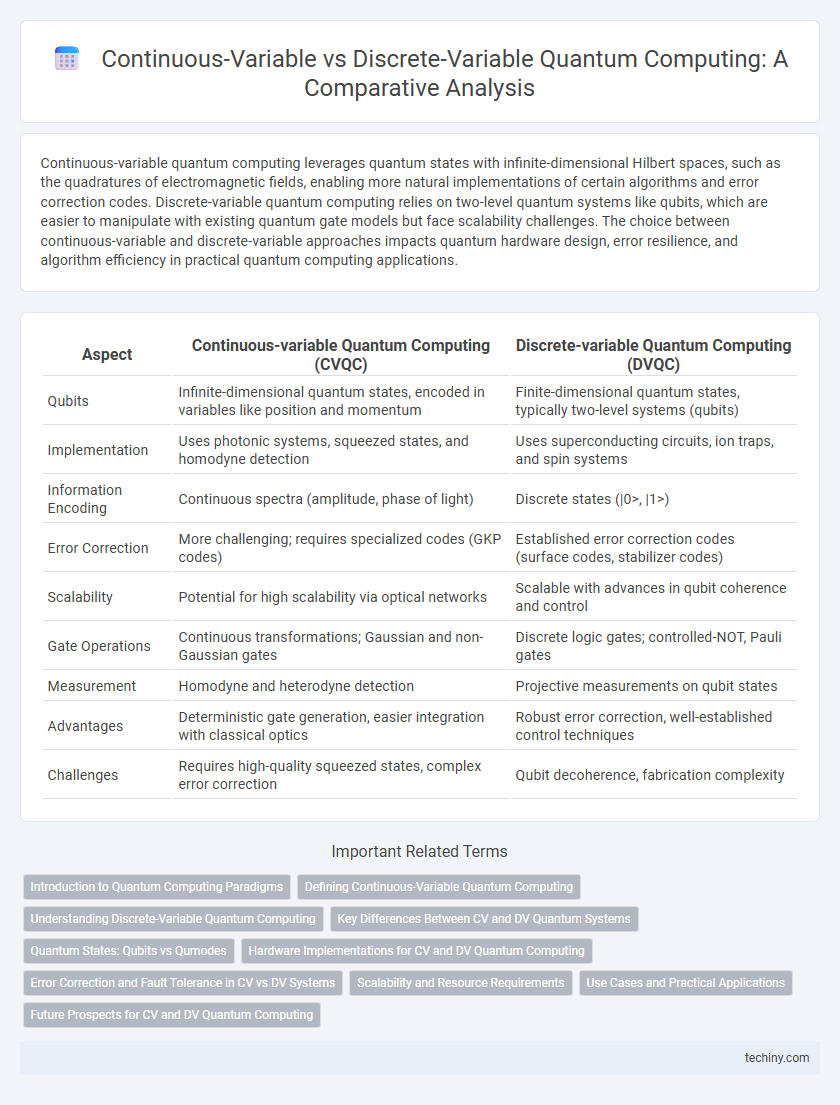
| Aspect | Continuous-variable Quantum Computing (CVQC) | Discrete-variable Quantum Computing (DVQC) |
|---|---|---|
| Qubits | Infinite-dimensional quantum states, encoded in variables like position and momentum | Finite-dimensional quantum states, typically two-level systems (qubits) |
| Implementation | Uses photonic systems, squeezed states, and homodyne detection | Uses superconducting circuits, ion traps, and spin systems |
| Information Encoding | Continuous spectra (amplitude, phase of light) | Discrete states (|0>, |1>) |
| Error Correction | More challenging; requires specialized codes (GKP codes) | Established error correction codes (surface codes, stabilizer codes) |
| Scalability | Potential for high scalability via optical networks | Scalable with advances in qubit coherence and control |
| Gate Operations | Continuous transformations; Gaussian and non-Gaussian gates | Discrete logic gates; controlled-NOT, Pauli gates |
| Measurement | Homodyne and heterodyne detection | Projective measurements on qubit states |
| Advantages | Deterministic gate generation, easier integration with classical optics | Robust error correction, well-established control techniques |
| Challenges | Requires high-quality squeezed states, complex error correction | Qubit decoherence, fabrication complexity |
Introduction to Quantum Computing Paradigms
Continuous-variable quantum computing utilizes quantum systems with infinite-dimensional Hilbert spaces, encoding information in variables like the quadratures of electromagnetic fields, enabling natural implementations of operations such as squeezing and homodyne detection. Discrete-variable quantum computing relies on finite-dimensional systems, primarily qubits, which represent information as discrete states through superposition and entanglement. These paradigms differ fundamentally in hardware design, error correction methods, and computational models, shaping diverse approaches to quantum algorithm development and practical realization.
Defining Continuous-Variable Quantum Computing
Continuous-variable quantum computing (CVQC) utilizes quantum systems described by continuous spectra, such as the position and momentum of light modes, enabling operations on infinite-dimensional Hilbert spaces. Unlike discrete-variable quantum computing that manipulates qubits with binary states, CVQC encodes information in continuous quantum variables, offering advantages in scalability and error correction. Quantum information in CVQC is processed using squeezed states and homodyne detection, making it particularly suitable for quantum communication and simulation tasks.
Understanding Discrete-Variable Quantum Computing
Discrete-variable quantum computing utilizes qubits, which exist in binary states of 0 and 1, enabling the implementation of quantum algorithms through quantum gates acting on individual qubits. This approach benefits from well-established error correction codes and solid physical qubit realizations in superconducting circuits and trapped ions. Understanding discrete-variable quantum computing is crucial for advancements in quantum processors that perform complex computations like Shor's and Grover's algorithms.
Key Differences Between CV and DV Quantum Systems
Continuous-variable (CV) quantum computing utilizes quantum states with infinite-dimensional Hilbert spaces, encoding information in quadratures of light, while discrete-variable (DV) quantum computing relies on finite-dimensional systems such as qubits represented by two-level states. CV systems offer advantages in scalability and deterministic gate operations through Gaussian states, whereas DV systems typically benefit from high-fidelity error correction and well-established qubit architectures. The measurement techniques also differ, with homodyne detection prominent in CV systems and projective measurements predominant in DV approaches.
Quantum States: Qubits vs Qumodes
Continuous-variable quantum computing utilizes qumodes, quantum states characterized by infinite-dimensional Hilbert spaces, enabling the encoding of information in variables like position and momentum. Discrete-variable quantum computing relies on qubits, which are two-level quantum systems representing binary information through superposition and entanglement. Qumodes offer advantages in scalability and implementation using optical systems, while qubits provide robust error correction and gate operation frameworks fundamental for quantum algorithms.
Hardware Implementations for CV and DV Quantum Computing
Continuous-variable (CV) quantum computing relies on quantum states encoded in infinite-dimensional systems like optical modes, implemented through hardware such as squeezed light sources, homodyne detectors, and optical parametric amplifiers. Discrete-variable (DV) quantum computing utilizes qubits typically realized in superconducting circuits, trapped ions, or quantum dots, each requiring precise gate operations and error correction protocols on two-level systems. The choice of hardware impacts scalability and noise resilience, with CV systems favoring photonic platforms offering room-temperature operation, while DV platforms demand cryogenic environments but benefit from established qubit control techniques.
Error Correction and Fault Tolerance in CV vs DV Systems
Continuous-variable (CV) quantum computing employs quantum states with infinite-dimensional Hilbert spaces, such as squeezed states of light, enabling natural error correction through bosonic codes like the Gottesman-Kitaev-Preskill (GKP) code, which correct small displacement errors effectively. Discrete-variable (DV) systems utilize qubits with two-level quantum states requiring complex stabilizer codes like surface codes that demand extensive physical qubits for logical qubit fault tolerance. CV systems show promise in reducing overhead for error correction and fault-tolerant operations, although they face challenges related to noise sensitivity and finite squeezing limitations compared to more mature DV approaches.
Scalability and Resource Requirements
Continuous-variable quantum computing employs quantum states with infinite-dimensional Hilbert spaces, enabling more scalable implementations through optical systems and fewer resource-intensive qubits. Discrete-variable quantum computing relies on two-level quantum bits (qubits), which often require complex error correction and high-fidelity operations, limiting scalability due to increased overhead. The resource demands for continuous-variable systems include squeezed light sources and homodyne detectors, offering practical advantages over the extensive ancilla qubits and gate operations needed in discrete-variable architectures.
Use Cases and Practical Applications
Continuous-variable quantum computing excels in quantum communication protocols such as quantum key distribution and quantum sensing, leveraging squeezed states of light for enhanced measurement precision. Discrete-variable quantum computing is primarily suited for complex quantum algorithms in cryptography, optimization, and error correction, implemented through qubit-based gate models. Practical applications differentiate as continuous-variable systems offer scalability in optical networks, while discrete-variable systems enable universal quantum computation for diverse computational problems.
Future Prospects for CV and DV Quantum Computing
Continuous-variable (CV) quantum computing offers scalability advantages through easier implementation of quantum error correction and compatibility with existing optical communication technologies, positioning it as a promising candidate for near-term quantum advantage. Discrete-variable (DV) quantum computing, leveraging well-established qubit-based frameworks and robust gate operations, continues to advance in fault-tolerant architectures and integration with superconducting and trapped-ion systems. Future prospects for both CV and DV quantum computing hinge on overcoming hardware limitations and developing hybrid approaches that combine the strengths of continuous and discrete variables to enhance computational power and error resilience.
Continuous-variable Quantum Computing vs Discrete-variable Quantum Computing Infographic
 techiny.com
techiny.com