The Variational Quantum Eigensolver (VQE) excels in solving quantum chemistry problems by approximating the ground state energy of molecules with hybrid quantum-classical approaches, leveraging parameterized quantum circuits and classical optimization. In contrast, the Quantum Approximate Optimization Algorithm (QAOA) targets combinatorial optimization challenges by encoding problems into quantum circuits that alternate between problem-specific and mixing Hamiltonians to find approximate solutions. Both algorithms utilize variational methods but differ in their application domains and circuit structures, with VQE tailored for eigenvalue problems and QAOA designed for discrete optimization tasks.
Table of Comparison
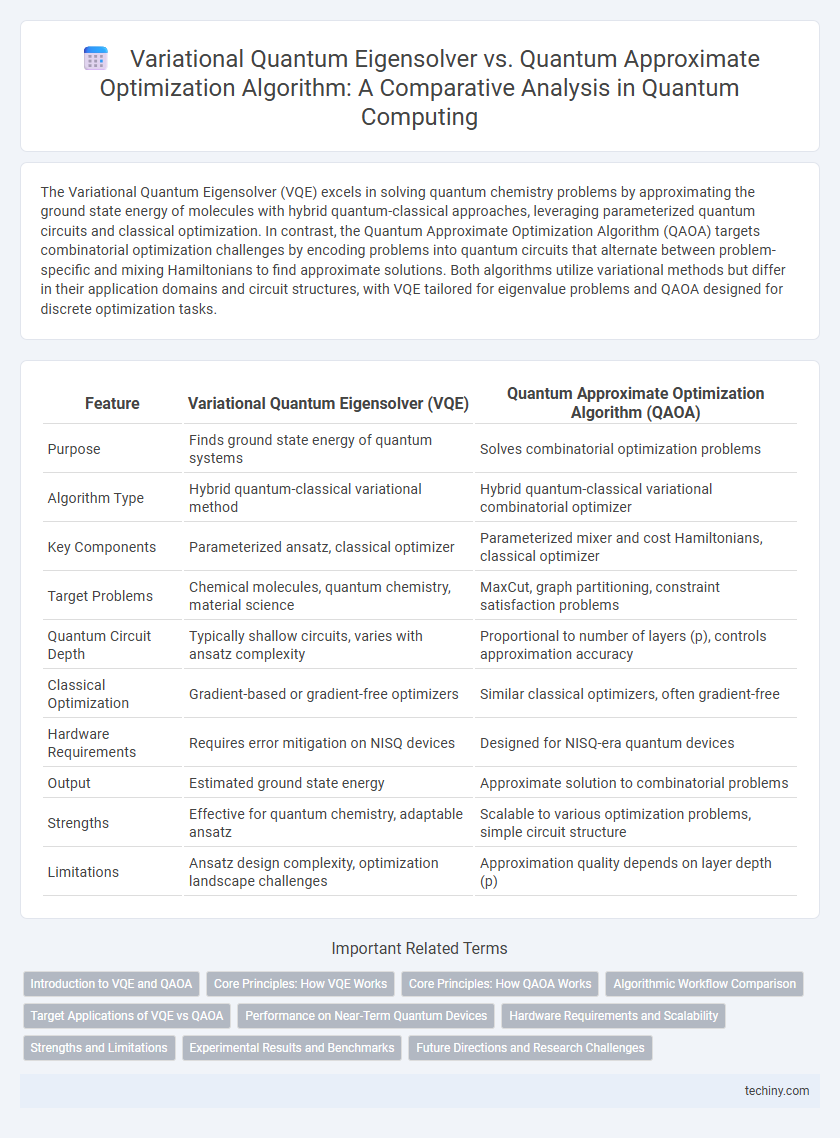
| Feature | Variational Quantum Eigensolver (VQE) | Quantum Approximate Optimization Algorithm (QAOA) |
|---|---|---|
| Purpose | Finds ground state energy of quantum systems | Solves combinatorial optimization problems |
| Algorithm Type | Hybrid quantum-classical variational method | Hybrid quantum-classical variational combinatorial optimizer |
| Key Components | Parameterized ansatz, classical optimizer | Parameterized mixer and cost Hamiltonians, classical optimizer |
| Target Problems | Chemical molecules, quantum chemistry, material science | MaxCut, graph partitioning, constraint satisfaction problems |
| Quantum Circuit Depth | Typically shallow circuits, varies with ansatz complexity | Proportional to number of layers (p), controls approximation accuracy |
| Classical Optimization | Gradient-based or gradient-free optimizers | Similar classical optimizers, often gradient-free |
| Hardware Requirements | Requires error mitigation on NISQ devices | Designed for NISQ-era quantum devices |
| Output | Estimated ground state energy | Approximate solution to combinatorial problems |
| Strengths | Effective for quantum chemistry, adaptable ansatz | Scalable to various optimization problems, simple circuit structure |
| Limitations | Ansatz design complexity, optimization landscape challenges | Approximation quality depends on layer depth (p) |
Introduction to VQE and QAOA
Variational Quantum Eigensolver (VQE) leverages a hybrid quantum-classical approach to find the ground state energy of molecular Hamiltonians by optimizing parameterized quantum circuits, making it effective for quantum chemistry problems. Quantum Approximate Optimization Algorithm (QAOA) targets combinatorial optimization tasks by encoding problem constraints into a cost Hamiltonian and iteratively applying quantum gates to approximate optimal solutions. Both algorithms utilize variational principles but differ in application focus, with VQE excelling in eigenvalue estimation and QAOA optimized for combinatorial problem solving on near-term quantum devices.
Core Principles: How VQE Works
The Variational Quantum Eigensolver (VQE) operates by leveraging a hybrid quantum-classical approach to find the ground state energy of a Hamiltonian, using parameterized quantum circuits to prepare trial states and a classical optimizer to minimize the measured energy. VQE relies on the variational principle, ensuring the energy estimate is always an upper bound to the true ground state, making it suitable for quantum chemistry simulations. Its efficiency comes from shallow quantum circuits and iterative refinement, which mitigate quantum noise on near-term quantum devices.
Core Principles: How QAOA Works
Quantum Approximate Optimization Algorithm (QAOA) operates by encoding combinatorial optimization problems into quantum states through parameterized quantum circuits, which are iteratively optimized via classical feedback loops. The algorithm alternates between applying problem-specific phase operators and mixing operators to evolve the quantum state toward high-quality approximate solutions. This hybrid quantum-classical approach leverages quantum superposition and interference to explore the solution space efficiently, distinguishing QAOA from the Variational Quantum Eigensolver's focus on eigenvalue problems.
Algorithmic Workflow Comparison
Variational Quantum Eigensolver (VQE) employs a hybrid quantum-classical loop to minimize the expectation value of a Hamiltonian, iteratively optimizing parameterized quantum circuits to approximate ground state energies. Quantum Approximate Optimization Algorithm (QAOA) alternates between applying problem-specific and mixing Hamiltonians through parameterized unitary operations, optimizing these parameters to find approximate solutions to combinatorial optimization problems. VQE focuses on energy minimization in quantum chemistry, while QAOA targets discrete optimization tasks, with both algorithms relying on classical optimizers but differing in circuit structure and objective formulation.
Target Applications of VQE vs QAOA
Variational Quantum Eigensolver (VQE) primarily targets quantum chemistry and material science applications by efficiently estimating ground state energies of molecular systems, aiding in drug discovery and catalyst design. Quantum Approximate Optimization Algorithm (QAOA) focuses on solving combinatorial optimization problems such as Max-Cut, Max-SAT, and other NP-hard problems relevant to logistics, finance, and machine learning. Both algorithms leverage parameterized quantum circuits but differ in application scope, with VQE excelling in continuous optimization and QAOA in discrete optimization challenges.
Performance on Near-Term Quantum Devices
Variational Quantum Eigensolver (VQE) demonstrates superior noise resilience and lower qubit depth requirements compared to Quantum Approximate Optimization Algorithm (QAOA), making it more suitable for near-term quantum devices with limited coherence times. VQE's adaptive parameter optimization enables effective handling of hardware imperfections while QAOA often demands deeper circuits that exacerbate error rates. Performance benchmarks reveal VQE achieves higher fidelity results on current NISQ devices for problems like molecular energy estimation and combinatorial optimization.
Hardware Requirements and Scalability
Variational Quantum Eigensolver (VQE) demands fewer qubits and lower circuit depth, making it more suitable for near-term noisy intermediate-scale quantum (NISQ) hardware, while Quantum Approximate Optimization Algorithm (QAOA) typically requires deeper circuits and more qubits to achieve better approximation ratios. VQE's hybrid quantum-classical approach leverages classical optimizers, enabling efficient scalability on current quantum devices with limited coherence times. In contrast, QAOA faces greater scalability challenges due to hardware constraints such as qubit connectivity and error rates, impacting its performance on larger problem instances.
Strengths and Limitations
Variational Quantum Eigensolver (VQE) excels in finding ground state energies of molecular systems with high accuracy, leveraging hybrid quantum-classical optimization to mitigate noise effects in near-term quantum devices. Quantum Approximate Optimization Algorithm (QAOA) targets combinatorial optimization problems, balancing circuit depth and approximation quality but often demands deeper circuits that increase sensitivity to decoherence and gate errors. While VQE shows versatility in chemistry and material science, its scalability is constrained by classical optimizer performance, whereas QAOA's effectiveness depends on the problem structure and may require heuristic tuning for optimal results.
Experimental Results and Benchmarks
Variational Quantum Eigensolver (VQE) and Quantum Approximate Optimization Algorithm (QAOA) both show promising experimental results in solving combinatorial optimization and quantum chemistry problems on near-term quantum devices. Benchmarks indicate VQE excels in finding ground state energies of molecular systems with higher accuracy, while QAOA demonstrates competitive performance for combinatorial optimization problems, especially Max-Cut. Experimental implementations reveal that noise sensitivity and circuit depth critically impact the scalability and fidelity of both algorithms, with ongoing research targeting error mitigation and hardware-efficient ansatz design.
Future Directions and Research Challenges
Variational Quantum Eigensolver (VQE) and Quantum Approximate Optimization Algorithm (QAOA) face challenges including scalability, error mitigation, and hardware noise resilience critical for future quantum advantage. Advancements in quantum hardware stability, algorithmic parameter optimization, and hybrid classical-quantum approaches represent key research directions to enhance their performance on near-term quantum devices. Exploration of problem-specific ansatz design and integration with machine learning techniques offers promising pathways for overcoming current limitations in solving complex optimization and quantum chemistry problems.
Variational Quantum Eigensolver vs Quantum Approximate Optimization Algorithm Infographic
 techiny.com
techiny.com