Grover's algorithm offers a quadratic speedup over classical search algorithms, enabling the search of an unsorted database in approximately N steps compared to N steps classically. This quantum advantage stems from amplitude amplification, which significantly reduces the number of queries required to find a desired item. Classical search algorithms rely on examining each element sequentially, making them less efficient for large datasets where Grover's algorithm excels.
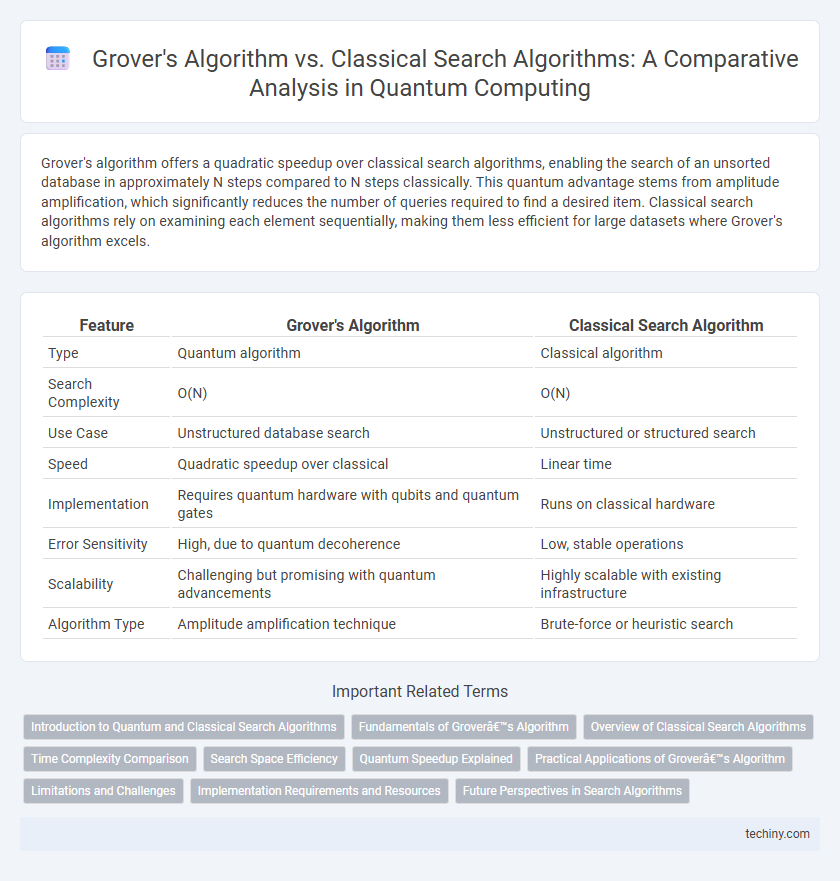
Table of Comparison
| Feature | Grover's Algorithm | Classical Search Algorithm |
|---|---|---|
| Type | Quantum algorithm | Classical algorithm |
| Search Complexity | O(N) | O(N) |
| Use Case | Unstructured database search | Unstructured or structured search |
| Speed | Quadratic speedup over classical | Linear time |
| Implementation | Requires quantum hardware with qubits and quantum gates | Runs on classical hardware |
| Error Sensitivity | High, due to quantum decoherence | Low, stable operations |
| Scalability | Challenging but promising with quantum advancements | Highly scalable with existing infrastructure |
| Algorithm Type | Amplitude amplification technique | Brute-force or heuristic search |
Introduction to Quantum and Classical Search Algorithms
Grover's algorithm provides a quadratic speedup over classical unstructured search algorithms by leveraging quantum superposition and amplitude amplification to locate a target item within an unsorted database of N elements in approximately O(N) time, compared to O(N) time for classical linear search. Classical search algorithms rely on sequential or exhaustive checking, requiring each element to be tested individually, leading to linear time complexity. Quantum search introduces probabilistic outcomes with high success probability, offering a fundamental computational advantage in database and optimization problems.
Fundamentals of Grover’s Algorithm
Grover's Algorithm leverages quantum superposition and amplitude amplification to search an unsorted database of N elements in approximately N steps, significantly faster than the classical linear search time of O(N). The core mechanism involves iteratively applying the Grover operator, which increases the probability amplitude of the target state while decreasing others, enabling a quantum system to find the desired element with high probability. This quadratic speedup arises from the principles of quantum parallelism and interference, distinguishing Grover's approach from classical search algorithms.
Overview of Classical Search Algorithms
Classical search algorithms, such as linear search and binary search, operate by sequentially or systematically checking each element in a dataset until the desired item is found. Linear search has a time complexity of O(n), requiring a scan through all n elements in the worst case, while binary search achieves O(log n) by repeatedly dividing the sorted dataset in half. These algorithms form the baseline for comparison against Grover's quantum search algorithm, which offers a quadratic speedup by searching unsorted databases in O(n) time.
Time Complexity Comparison
Grover's Algorithm achieves a quadratic speedup over classical search algorithms by solving unstructured database search problems with a time complexity of O(N) compared to O(N) for classical linear search. While classical algorithms require examining each element sequentially in the worst case, Grover's Algorithm leverages quantum amplitude amplification to reduce the number of required queries significantly. This difference enables faster search on large datasets, highlighting a key advantage of quantum computing in optimization and search tasks.
Search Space Efficiency
Grover's Algorithm significantly improves search space efficiency by providing a quadratic speedup over classical search algorithms, reducing the search complexity from O(N) to O(N) for unsorted databases. This quantum algorithm leverages superposition and amplitude amplification to locate a target item with fewer queries compared to linear classical methods. The efficiency gain becomes increasingly impactful as the search space size grows, highlighting Grover's advantage in handling large-scale unstructured search problems.
Quantum Speedup Explained
Grover's Algorithm provides a quadratic speedup over classical search algorithms by reducing the search complexity from O(N) to O(N), where N is the number of unsorted entries. This quantum speedup is achieved through amplitude amplification, which amplifies the probability of the correct solution within a superposition of all possible states. As a result, Grover's Algorithm significantly improves efficiency in unstructured search problems compared to classical brute-force methods.
Practical Applications of Grover’s Algorithm
Grover's Algorithm offers a quadratic speedup in unsorted database search problems, reducing the complexity from O(N) in classical search algorithms to O(N), which significantly enhances efficiency in cryptographic key searching and optimization tasks. Practical applications include accelerating brute-force attacks on symmetric key cryptosystems and speeding up pattern matching in large unstructured datasets. This quantum advantage can transform fields like cybersecurity, logistics, and machine learning by enabling faster data retrieval and problem-solving capabilities.
Limitations and Challenges
Grover's Algorithm offers a quadratic speedup over classical search algorithms, reducing search time from O(N) to O(N) in unsorted databases. However, its efficiency is limited by the requirement of a large number of qubits with low error rates and the complexity of implementing quantum oracle functions. Classical search algorithms, while slower, are more practical for current hardware due to robust error correction and scalability in classical computing systems.
Implementation Requirements and Resources
Grover's Algorithm requires a quantum computer with multiple qubits capable of maintaining coherence and executing a sequence of oracle and diffusion operations, demanding precise quantum gate control and error correction mechanisms. In contrast, classical search algorithms operate on conventional digital hardware with linear time complexity, relying solely on classical memory and processing units without the need for quantum error correction. Implementation of Grover's Algorithm typically involves significant overhead in quantum circuit depth and qubit connectivity, whereas classical algorithms prioritize algorithmic simplicity and scalability on existing computational infrastructure.
Future Perspectives in Search Algorithms
Grover's Algorithm offers a quadratic speedup over classical search algorithms, reducing search time from O(N) to O(N), which holds significant potential for future advancements in database querying and cryptanalysis. As quantum hardware continues to evolve, integrating Grover's Algorithm into hybrid quantum-classical frameworks could revolutionize search efficiency across large, unstructured datasets. Ongoing research aims to optimize error correction and algorithmic implementation, paving the way for practical quantum-enhanced search solutions beyond the limitations of classical computing.
Grover’s Algorithm vs Classical Search Algorithm Infographic
 techiny.com
techiny.com