Phase flip errors alter the phase of a qubit without changing its state vector's computational basis, causing a sign change that impacts quantum interference. Bit flip errors invert the qubit state from |0> to |1> or vice versa, directly affecting the stored information. Understanding the distinction between phase flip and bit flip errors is crucial for designing effective quantum error correction codes that maintain qubit coherence.
Table of Comparison
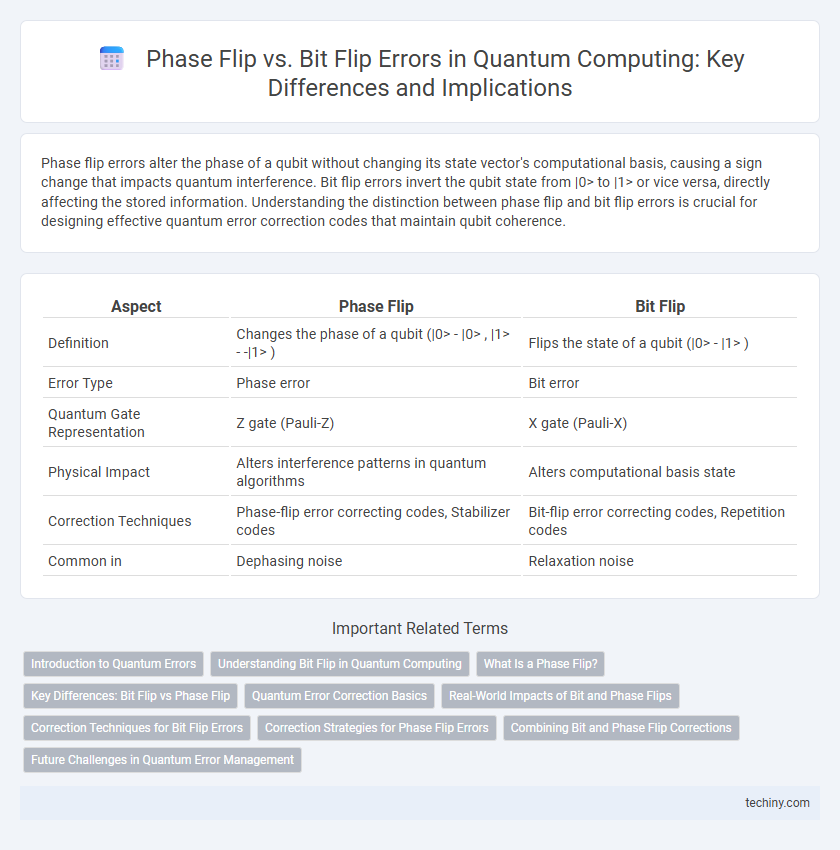
| Aspect | Phase Flip | Bit Flip |
|---|---|---|
| Definition | Changes the phase of a qubit (|0> - |0> , |1> - -|1> ) | Flips the state of a qubit (|0> - |1> ) |
| Error Type | Phase error | Bit error |
| Quantum Gate Representation | Z gate (Pauli-Z) | X gate (Pauli-X) |
| Physical Impact | Alters interference patterns in quantum algorithms | Alters computational basis state |
| Correction Techniques | Phase-flip error correcting codes, Stabilizer codes | Bit-flip error correcting codes, Repetition codes |
| Common in | Dephasing noise | Relaxation noise |
Introduction to Quantum Errors
Quantum errors are critical challenges in quantum computing, where phase flip and bit flip represent two fundamental types. Bit flip errors occur when a qubit's state changes from |0> to |1> or vice versa, while phase flip errors invert the phase of the qubit's state without altering its computational basis. Understanding and correcting these errors through quantum error correction codes is essential for reliable quantum information processing.
Understanding Bit Flip in Quantum Computing
Bit flip errors in quantum computing occur when a qubit state |0> changes to |1> or vice versa, representing a fundamental type of quantum noise. Understanding bit flip is crucial for designing quantum error correction codes like the Shor code or the three-qubit bit-flip code, which detect and correct these errors to maintain qubit coherence. Effective mitigation of bit flip errors enables more reliable quantum computation, enhancing gate fidelity and overall quantum circuit performance.
What Is a Phase Flip?
A phase flip in quantum computing refers to a quantum error that changes the phase of a qubit without altering its amplitude, represented by the Z Pauli operator. Unlike a bit flip, which changes the state from |0> to |1> or vice versa, a phase flip changes the relative phase by applying a negative sign to the |1> component, transforming |ps> = a|0> + b|1> into a|0> - b|1> . Detecting and correcting phase flips is critical for maintaining coherence and error mitigation in quantum error correction codes like the Shor or Steane codes.
Key Differences: Bit Flip vs Phase Flip
Bit flip errors invert the computational basis states, changing |0> to |1> and vice versa, while phase flip errors alter the relative phase between states by flipping the sign of the |1> component in superposition. Bit flip errors correspond to the Pauli-X operator acting on qubits, whereas phase flips correspond to the Pauli-Z operator. Quantum error correction codes often handle these errors distinctly, requiring different syndromes to detect and correct bit flips and phase flips effectively.
Quantum Error Correction Basics
Phase flip and bit flip errors represent fundamental quantum noise types affecting qubits' coherence and computational accuracy. Quantum error correction codes, such as the Shor or Steane codes, utilize entanglement and syndrome measurement to detect and correct these errors without collapsing the quantum state. Effective correction of phase flip and bit flip errors is crucial to maintaining fault tolerance and enabling scalable quantum computing.
Real-World Impacts of Bit and Phase Flips
Bit flips and phase flips represent common quantum errors, with bit flips altering qubit states and phase flips modifying their phase information. In practical quantum computing, bit flips can cause incorrect computational outputs, severely impacting algorithms like Grover's search or Shor's factoring. Phase flips disrupt the relative phase coherence crucial for quantum interference, affecting error correction protocols and diminishing the fidelity of quantum communication and cryptography systems.
Correction Techniques for Bit Flip Errors
Bit flip error correction in quantum computing primarily relies on the three-qubit repetition code, which encodes a logical qubit into three physical qubits to detect and correct single bit flip errors. Syndrome measurement circuits identify error locations by comparing qubit states without collapsing quantum information, enabling precise recovery operations. Advanced techniques extend this approach by integrating entanglement and stabilizer codes, enhancing fault tolerance against bit-flip errors in noisy quantum environments.
Correction Strategies for Phase Flip Errors
Phase flip error correction in quantum computing primarily employs the Shor and Steane codes, which encode a single qubit into multiple physical qubits to detect and correct phase flips without collapsing the quantum state. These quantum error-correcting codes leverage entanglement and syndrome measurement to identify phase errors while preserving coherence. Stabilizer codes, particularly CSS codes, effectively separate phase flip error correction from bit flip errors, optimizing fault-tolerant quantum computation.
Combining Bit and Phase Flip Corrections
Combining bit flip and phase flip corrections enhances quantum error correction by simultaneously addressing both X and Z errors within qubits. Techniques such as the Shor code and surface codes employ this integrated approach to preserve quantum information against decoherence and operational faults. This synergistic correction strategy is essential for improving the fidelity and stability of quantum computations in noisy environments.
Future Challenges in Quantum Error Management
Phase flip and bit flip errors represent fundamental challenges in quantum error management that demand sophisticated correction protocols. Future advancements require developing more robust quantum error-correcting codes capable of simultaneously detecting and correcting both types of errors with minimal resource overhead. Scaling these methods efficiently in larger quantum systems remains a critical obstacle to achieving fault-tolerant quantum computing.
Phase Flip vs Bit Flip Infographic
 techiny.com
techiny.com