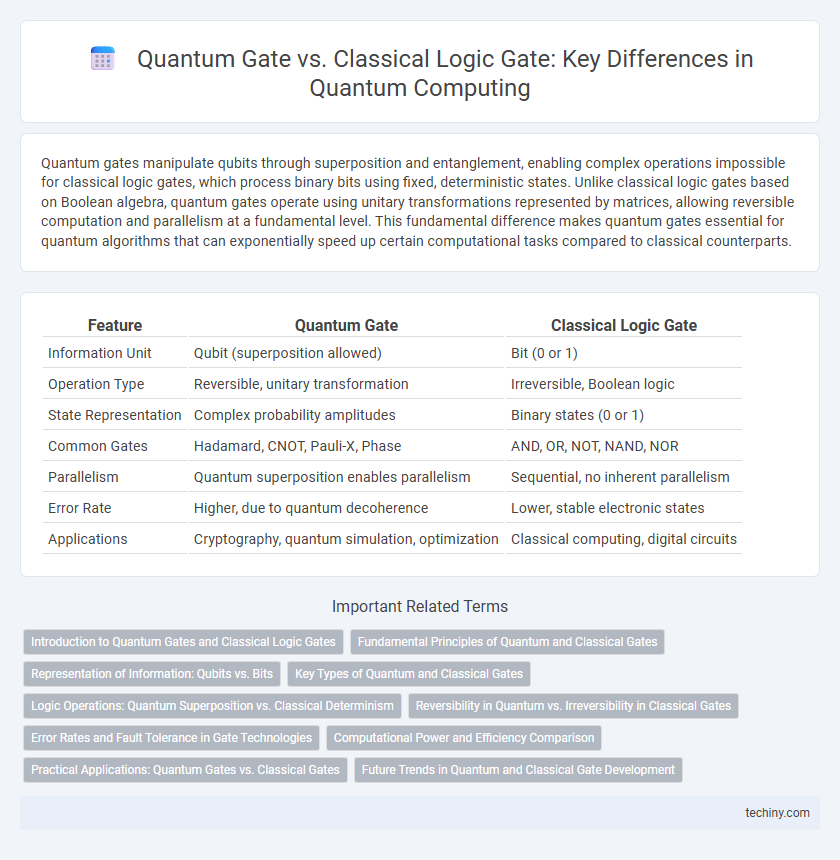
Quantum gates manipulate qubits through superposition and entanglement, enabling complex operations impossible for classical logic gates, which process binary bits using fixed, deterministic states. Unlike classical logic gates based on Boolean algebra, quantum gates operate using unitary transformations represented by matrices, allowing reversible computation and parallelism at a fundamental level. This fundamental difference makes quantum gates essential for quantum algorithms that can exponentially speed up certain computational tasks compared to classical counterparts.
Table of Comparison
| Feature | Quantum Gate | Classical Logic Gate |
|---|---|---|
| Information Unit | Qubit (superposition allowed) | Bit (0 or 1) |
| Operation Type | Reversible, unitary transformation | Irreversible, Boolean logic |
| State Representation | Complex probability amplitudes | Binary states (0 or 1) |
| Common Gates | Hadamard, CNOT, Pauli-X, Phase | AND, OR, NOT, NAND, NOR |
| Parallelism | Quantum superposition enables parallelism | Sequential, no inherent parallelism |
| Error Rate | Higher, due to quantum decoherence | Lower, stable electronic states |
| Applications | Cryptography, quantum simulation, optimization | Classical computing, digital circuits |
Introduction to Quantum Gates and Classical Logic Gates
Quantum gates manipulate qubits using principles of superposition and entanglement, enabling complex quantum computations beyond classical capabilities. Classical logic gates, such as AND, OR, and NOT, operate on binary bits with deterministic outputs, forming the foundation of traditional digital circuits. Quantum gates like the Hadamard, Pauli-X, and CNOT perform reversible transformations essential for quantum algorithms, contrasting with the irreversible nature of most classical logic gates.
Fundamental Principles of Quantum and Classical Gates
Quantum gates operate on qubits using principles of superposition and entanglement, enabling simultaneous processing of multiple states through unitary transformations. Classical logic gates manipulate binary bits in deterministic, irreversible operations based on Boolean algebra, such as AND, OR, and NOT functions. The fundamental difference lies in quantum gates preserving complex probability amplitudes and reversibility, whereas classical gates produce definitive output values without exploiting quantum coherence.
Representation of Information: Qubits vs. Bits
Quantum gates manipulate qubits, which represent information using superposition and entanglement, allowing multiple states simultaneously. Classical logic gates operate on bits that are strictly binary, holding either 0 or 1 at any time. This fundamental difference enables quantum gates to perform complex computations more efficiently than classical gates in certain algorithms.
Key Types of Quantum and Classical Gates
Quantum gates such as the Hadamard, Pauli-X, and CNOT gates manipulate qubits through superposition and entanglement, enabling complex quantum algorithms, while classical logic gates like AND, OR, and NOT operate on binary bits using deterministic Boolean logic. The Hadamard gate creates equal superposition states, the Pauli-X gate functions as a quantum bit-flip, and the CNOT gate performs conditional operations essential for entanglement. Classical gates rely on fixed truth tables, whereas quantum gates utilize unitary transformations preserving quantum coherence.
Logic Operations: Quantum Superposition vs. Classical Determinism
Quantum gates operate on qubits, enabling quantum superposition where a qubit can represent both 0 and 1 simultaneously, vastly increasing computational parallelism. Classical logic gates process bits in a deterministic manner, with each bit strictly as 0 or 1, limiting operations to fixed binary states. This fundamental difference allows quantum gates to perform complex logic operations that classical gates cannot achieve efficiently.
Reversibility in Quantum vs. Irreversibility in Classical Gates
Quantum gates are inherently reversible, allowing the retrieval of input states from outputs due to their unitary nature, which preserves information and enables quantum error correction. Classical logic gates like AND, OR, and NAND are irreversible, causing information loss by mapping multiple input states to a single output, leading to heat dissipation in computation. Reversibility in quantum gates underpins key quantum computing principles, such as entanglement manipulation and superposition preservation, which classical gates cannot achieve.
Error Rates and Fault Tolerance in Gate Technologies
Quantum gates exhibit higher error rates compared to classical logic gates due to qubit decoherence and quantum noise, challenging reliable computation. Fault tolerance in quantum gate technologies is addressed through quantum error correction codes like the surface code, which requires significant qubit overhead to maintain logical gate fidelity. Classical logic gates benefit from mature fault-tolerant designs and semiconductor stability, resulting in error rates orders of magnitude lower than current quantum counterparts.
Computational Power and Efficiency Comparison
Quantum gates leverage qubits' superposition and entanglement, enabling parallel computation and exponentially increasing computational power compared to classical logic gates, which operate on binary bits with deterministic outputs. This intrinsic parallelism allows quantum gates to solve complex problems like factoring and search algorithms with significantly higher efficiency and reduced time complexity. In contrast, classical gates are limited by sequential processing and scaling issues, making quantum gates fundamentally superior in handling large-scale computations.
Practical Applications: Quantum Gates vs. Classical Gates
Quantum gates manipulate qubits using superposition and entanglement, enabling complex computations such as quantum cryptography, optimization problems, and molecular simulations that classical gates cannot efficiently solve. Classical logic gates operate on binary bits with deterministic outputs, suitable for conventional digital circuits, microprocessors, and data storage systems. Practical applications of quantum gates surpass classical gates in fields requiring massive parallelism and quantum advantage, driving advancements in cryptographic security and drug discovery.
Future Trends in Quantum and Classical Gate Development
Quantum gates operate on qubits using superposition and entanglement, enabling exponentially higher computational power compared to classical logic gates that manipulate binary bits. Future trends in quantum gate development focus on error correction, scalability, and fault-tolerant architectures to enhance quantum processor stability and performance. Classical gate evolution continues with advancements in semiconductor materials and nanoscale fabrication to push computing speeds and energy efficiency in traditional digital circuits.
Quantum Gate vs Classical Logic Gate Infographic
 techiny.com
techiny.com