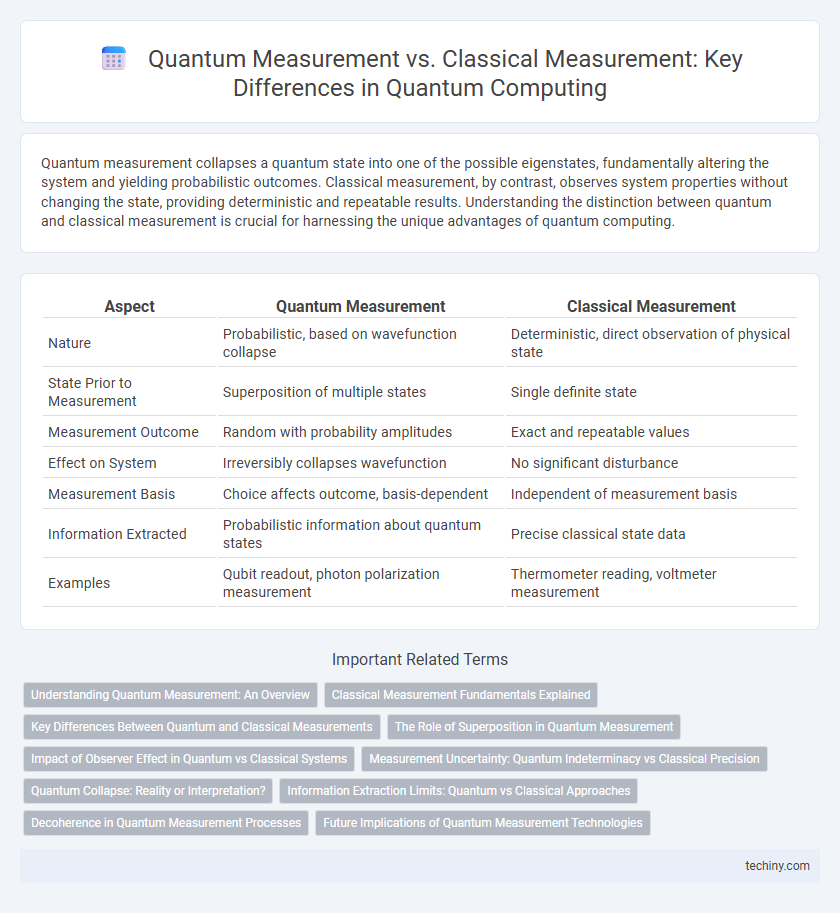
Quantum measurement collapses a quantum state into one of the possible eigenstates, fundamentally altering the system and yielding probabilistic outcomes. Classical measurement, by contrast, observes system properties without changing the state, providing deterministic and repeatable results. Understanding the distinction between quantum and classical measurement is crucial for harnessing the unique advantages of quantum computing.
Table of Comparison
| Aspect | Quantum Measurement | Classical Measurement |
|---|---|---|
| Nature | Probabilistic, based on wavefunction collapse | Deterministic, direct observation of physical state |
| State Prior to Measurement | Superposition of multiple states | Single definite state |
| Measurement Outcome | Random with probability amplitudes | Exact and repeatable values |
| Effect on System | Irreversibly collapses wavefunction | No significant disturbance |
| Measurement Basis | Choice affects outcome, basis-dependent | Independent of measurement basis |
| Information Extracted | Probabilistic information about quantum states | Precise classical state data |
| Examples | Qubit readout, photon polarization measurement | Thermometer reading, voltmeter measurement |
Understanding Quantum Measurement: An Overview
Quantum measurement collapses a superposition of quantum states into a single eigenstate, fundamentally differing from classical measurement that reveals pre-existing values without altering the system. The probabilistic nature of quantum measurement is governed by the Born rule, where outcomes are determined by the wave function's amplitude squared. This process introduces inherent uncertainty and decoherence, making quantum measurement a critical challenge in quantum computing and information processing.
Classical Measurement Fundamentals Explained
Classical measurement relies on deterministic processes where observable properties, such as voltage or position, are directly quantified without altering the state being measured. It is governed by classical physics principles, allowing repeatable and precise readings based on well-defined variables. In contrast to quantum measurement, classical systems do not experience wavefunction collapse, ensuring measurements are non-invasive and outcomes consistent over multiple observations.
Key Differences Between Quantum and Classical Measurements
Quantum measurement collapses a quantum system's wavefunction into a definite state, making outcomes inherently probabilistic and non-deterministic, unlike classical measurement which observes predefined properties with deterministic precision. Quantum measurements often disturb the system due to the observer effect, whereas classical measurements can, in principle, be performed without influencing the system's state. Furthermore, quantum measurements reveal superposition and entanglement phenomena, key features absent in classical measurement frameworks.
The Role of Superposition in Quantum Measurement
Quantum measurement fundamentally differs from classical measurement through the concept of superposition, where a quantum system exists simultaneously in multiple states until observed. Superposition enables quantum bits (qubits) to represent both 0 and 1 concurrently, exponentially increasing computational power compared to classical bits. Measurement collapses the superposition into a definite state, making the probabilistic nature of quantum outcomes a key aspect of quantum computing algorithms and error correction.
Impact of Observer Effect in Quantum vs Classical Systems
Quantum measurement fundamentally differs from classical measurement due to the observer effect, where the act of observing directly influences the state of the quantum system, causing wavefunction collapse and altering the probabilities of outcomes. In classical systems, measurements can be made with negligible disturbance, allowing the system to be observed without significantly affecting its state. This distinction is crucial in quantum computing, where the observer effect limits information extraction and necessitates careful design of measurement protocols to preserve quantum coherence and enable reliable computation.
Measurement Uncertainty: Quantum Indeterminacy vs Classical Precision
Quantum measurement is characterized by inherent uncertainty due to quantum indeterminacy, where the act of measuring collapses a superposition of states into a definite outcome, limiting precision. Classical measurement operates under deterministic principles, allowing for high precision and repeatability with negligible uncertainty in most cases. The fundamental difference arises because quantum systems obey probabilistic wavefunctions, whereas classical systems are governed by fixed variables, resulting in a fundamental limit to measurement accuracy in quantum computing.
Quantum Collapse: Reality or Interpretation?
Quantum measurement induces wavefunction collapse, a phenomenon where quantum superpositions reduce to a definite state upon observation, contrasting with classical measurement's deterministic outcomes. The debate centers on whether collapse represents a physical reality or is merely an interpretative tool within quantum mechanics, with interpretations like Copenhagen asserting its fundamental role while others like Many-Worlds deny physical collapse altogether. Experimental evidence of phenomena such as quantum decoherence challenges the notion of objective collapse, suggesting collapse might emerge from system-environment interactions rather than an intrinsic physical process.
Information Extraction Limits: Quantum vs Classical Approaches
Quantum measurement fundamentally differs from classical measurement in its ability to extract information due to the principles of superposition and entanglement, which allow quantum systems to encode exponentially more information than classical counterparts. However, quantum measurement is constrained by the collapse of the quantum state, limiting the retrievable information to probabilistic outcomes rather than definite values. Classical measurement accesses deterministic data directly, but it cannot exploit quantum parallelism, resulting in fundamentally lower limits on information extraction efficiency compared to quantum approaches.
Decoherence in Quantum Measurement Processes
Quantum measurement fundamentally differs from classical measurement due to the phenomenon of decoherence, which causes a quantum system to lose its coherent superposition states when interacting with the environment. Decoherence rapidly destroys quantum information by entangling the measured system with external degrees of freedom, effectively collapsing the wavefunction into a classical probabilistic mixture. This transition from quantum to classical behavior poses significant challenges for maintaining quantum coherence during measurement and is a critical barrier in developing reliable quantum computing technologies.
Future Implications of Quantum Measurement Technologies
Quantum measurement technologies promise to revolutionize data processing by enabling the collapse of qubits into specific states, vastly enhancing computational speed and accuracy compared to classical measurement methods. Future advancements will drive quantum error correction improvements, crucial for developing scalable quantum computers capable of solving complex problems beyond classical capabilities. These breakthroughs will influence cryptography, optimization algorithms, and material science, transforming industries and scientific research globally.
Quantum Measurement vs Classical Measurement Infographic
 techiny.com
techiny.com