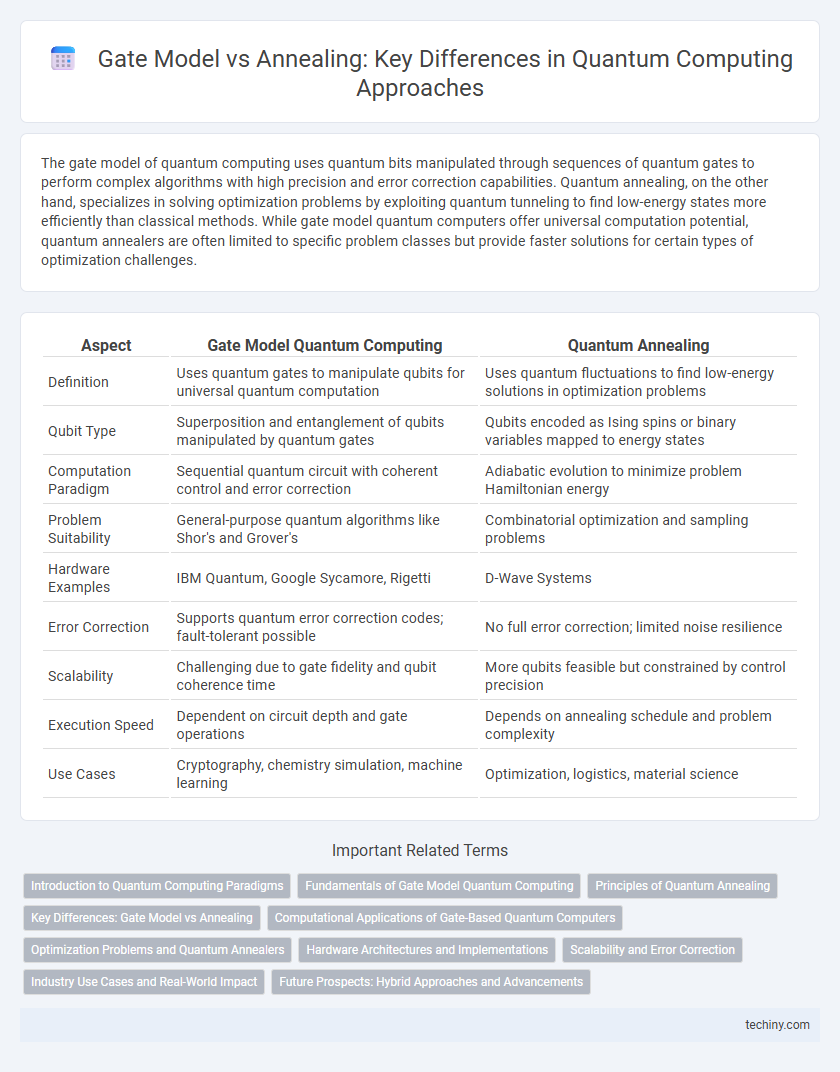
The gate model of quantum computing uses quantum bits manipulated through sequences of quantum gates to perform complex algorithms with high precision and error correction capabilities. Quantum annealing, on the other hand, specializes in solving optimization problems by exploiting quantum tunneling to find low-energy states more efficiently than classical methods. While gate model quantum computers offer universal computation potential, quantum annealers are often limited to specific problem classes but provide faster solutions for certain types of optimization challenges.
Table of Comparison
| Aspect | Gate Model Quantum Computing | Quantum Annealing |
|---|---|---|
| Definition | Uses quantum gates to manipulate qubits for universal quantum computation | Uses quantum fluctuations to find low-energy solutions in optimization problems |
| Qubit Type | Superposition and entanglement of qubits manipulated by quantum gates | Qubits encoded as Ising spins or binary variables mapped to energy states |
| Computation Paradigm | Sequential quantum circuit with coherent control and error correction | Adiabatic evolution to minimize problem Hamiltonian energy |
| Problem Suitability | General-purpose quantum algorithms like Shor's and Grover's | Combinatorial optimization and sampling problems |
| Hardware Examples | IBM Quantum, Google Sycamore, Rigetti | D-Wave Systems |
| Error Correction | Supports quantum error correction codes; fault-tolerant possible | No full error correction; limited noise resilience |
| Scalability | Challenging due to gate fidelity and qubit coherence time | More qubits feasible but constrained by control precision |
| Execution Speed | Dependent on circuit depth and gate operations | Depends on annealing schedule and problem complexity |
| Use Cases | Cryptography, chemistry simulation, machine learning | Optimization, logistics, material science |
Introduction to Quantum Computing Paradigms
Quantum computing paradigms primarily consist of the gate model and quantum annealing, each leveraging different mechanisms to solve complex problems. The gate model uses a sequence of quantum gates to manipulate qubits through unitary operations, enabling universal quantum computation and algorithms like Shor's and Grover's. Quantum annealing exploits quantum tunneling to find low-energy states of optimization problems, making it well-suited for combinatorial problem-solving but limited in universality compared to the gate-based approach.
Fundamentals of Gate Model Quantum Computing
Gate model quantum computing relies on qubits manipulated through a sequence of quantum gates, enabling universal quantum algorithms by exploiting superposition and entanglement. It uses unitary transformations to perform precise, reversible operations on qubit states, allowing complex computations and error correction protocols. This fundamental approach contrasts with quantum annealing by targeting a broader range of computational problems using coherent gate-based circuits.
Principles of Quantum Annealing
Quantum annealing leverages quantum tunneling to find the global minimum of a problem's energy landscape by evolving a system from a superposition of all possible states toward the lowest-energy state. Unlike the gate model, which uses discrete quantum gates to perform computations through unitary transformations, quantum annealing continuously adjusts the Hamiltonian of the system to solve optimization problems. The process exploits quantum fluctuations to escape local minima, making it especially effective for combinatorial optimization and certain NP-hard problems.
Key Differences: Gate Model vs Annealing
Gate model quantum computers use discrete quantum gates to perform universal quantum operations through a sequence of controlled unitary transformations, enabling precise algorithmic execution and error correction. In contrast, quantum annealing leverages quantum fluctuations to find the global minimum of optimization problems by gradually evolving the system's Hamiltonian, specialized for combinatorial optimization rather than general-purpose computing. Key differences include gate model's suitability for complex algorithms like Shor's and Grover's with error correction capabilities, versus annealing's efficiency in solving specific optimization tasks on hardware such as D-Wave systems.
Computational Applications of Gate-Based Quantum Computers
Gate-based quantum computers leverage qubits manipulated through a series of quantum gates, enabling universal quantum computation suitable for complex algorithms like Shor's factoring and Grover's search. These devices excel in solving problems involving quantum error correction, cryptographic analysis, and simulation of quantum systems with intricate entanglement patterns. Compared to quantum annealing, gate-based systems offer greater algorithmic flexibility and scalability for broad computational applications in optimization, chemistry, and artificial intelligence.
Optimization Problems and Quantum Annealers
Quantum Annealers, such as those developed by D-Wave Systems, excel in solving combinatorial optimization problems by exploiting quantum tunneling to find low-energy states efficiently. The gate model quantum computers use quantum circuits and algorithms like Grover's to tackle optimization problems but often face scalability challenges compared to annealing approaches. Optimization problems involving complex energy landscapes benefit from quantum annealing's ability to escape local minima, making it a promising approach for real-world applications in logistics, finance, and machine learning.
Hardware Architectures and Implementations
Gate model quantum computers utilize superconducting qubits arranged in a lattice, enabling precise control through microwave pulses for universal quantum operations. Annealing quantum devices, like those developed by D-Wave, employ flux qubits embedded in a programmed energy landscape to solve optimization problems via quantum tunneling. The gate model architecture demands error correction for scalability, while annealing hardware prioritizes coherence time and connectivity to enhance problem-solving efficacy.
Scalability and Error Correction
Gate model quantum computers achieve scalability through modular qubit architectures and error-correcting codes like surface codes, enabling fault-tolerant operations despite hardware imperfections. Quantum annealing systems prioritize scalability by integrating thousands of qubits with less complex error correction, relying on physical system stability rather than active error correction codes. Error correction remains a critical challenge for gate model machines, demanding substantial overhead, while annealing methods tolerate certain errors inherently but face limitations in precision and coherence at scale.
Industry Use Cases and Real-World Impact
Gate model quantum computing excels in complex optimization, cryptography, and drug discovery, driving advancements in pharmaceuticals and secure communications. Quantum annealing specializes in solving large-scale combinatorial problems, making it effective for logistics, financial modeling, and material science simulations. Industry leaders like D-Wave and IBM deploy these technologies to innovate real-world solutions, accelerating problem-solving in sectors such as supply chain management and chemical engineering.
Future Prospects: Hybrid Approaches and Advancements
Hybrid quantum computing approaches that integrate gate model architectures with quantum annealing techniques are rapidly advancing, promising enhanced problem-solving capabilities across optimization and machine learning domains. Innovations in error correction and qubit coherence in gate model systems complement the scalability and hardware efficiency advantages of annealing methods, fostering new algorithms capable of tackling complex computational tasks. Continued progress in these hybrid frameworks is expected to accelerate commercial applications and quantum advantage realization in fields such as cryptography, drug discovery, and supply chain optimization.
gate model vs annealing Infographic
 techiny.com
techiny.com