Grover's Algorithm offers a quadratic speedup over brute-force search by reducing the required number of queries from O(N) to O(N), significantly enhancing search efficiency in unsorted databases. This quantum algorithm exploits superposition and amplitude amplification to find the desired item faster than classical methods. While brute-force search exhaustively checks each possibility, Grover's Algorithm leverages quantum parallelism, making it a powerful tool for solving complex search problems.
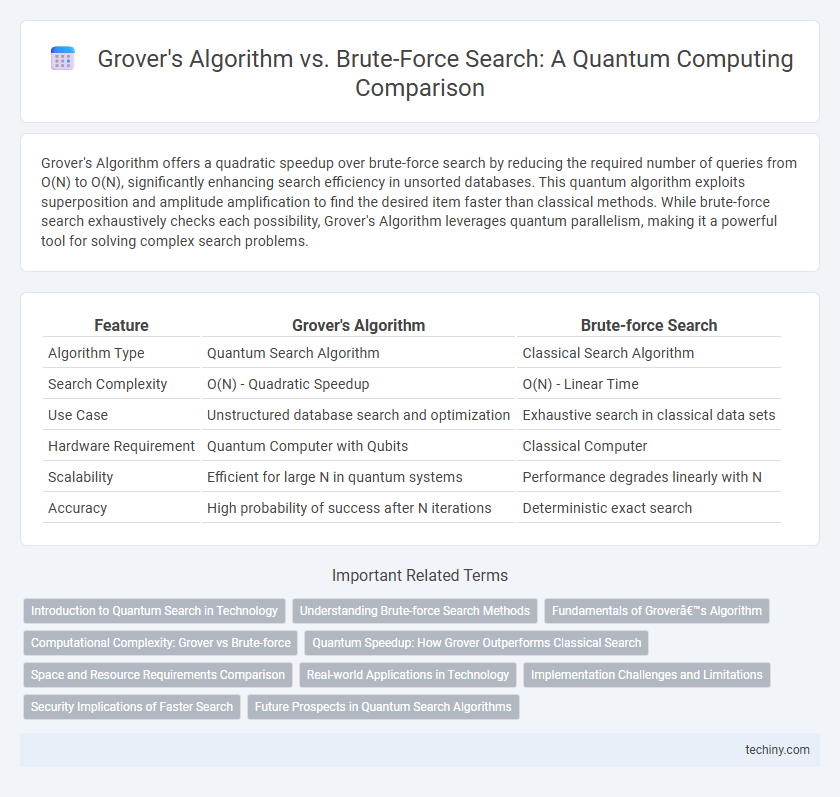
Table of Comparison
| Feature | Grover's Algorithm | Brute-force Search |
|---|---|---|
| Algorithm Type | Quantum Search Algorithm | Classical Search Algorithm |
| Search Complexity | O(N) - Quadratic Speedup | O(N) - Linear Time |
| Use Case | Unstructured database search and optimization | Exhaustive search in classical data sets |
| Hardware Requirement | Quantum Computer with Qubits | Classical Computer |
| Scalability | Efficient for large N in quantum systems | Performance degrades linearly with N |
| Accuracy | High probability of success after N iterations | Deterministic exact search |
Introduction to Quantum Search in Technology
Grover's Algorithm significantly enhances search efficiency by providing a quadratic speedup over classical brute-force search methods, reducing the time complexity from O(N) to O(N) for unstructured databases. This quantum search algorithm leverages superposition and amplitude amplification to locate a target item with fewer queries, making it a pivotal technique in quantum computing. Its implementation in various quantum technologies demonstrates promising advancements in database searching, cryptography, and optimization problems.
Understanding Brute-force Search Methods
Brute-force search methods systematically evaluate every possible solution in a problem space, making them computationally expensive and inefficient for large datasets with exponential growth. Grover's Algorithm, a quantum algorithm, offers a quadratic speedup by amplifying the probability of the correct solution in an unsorted database using quantum parallelism and interference. Unlike classical brute-force techniques, Grover's Algorithm significantly reduces the number of queries needed, from O(N) to O(N), highlighting its advantage in solving search problems more efficiently.
Fundamentals of Grover’s Algorithm
Grover's Algorithm leverages quantum superposition to search an unsorted database of N items in approximately N operations, providing a quadratic speedup over classical brute-force search, which requires O(N) steps. The algorithm uses amplitude amplification through iterative oracle queries and inversion about the mean to increase the probability of measuring the desired item. Its fundamental components include the oracle function, Grover diffusion operator, and the repeated application of these to amplify the target state's amplitude efficiently.
Computational Complexity: Grover vs Brute-force
Grover's algorithm achieves a quadratic speedup over brute-force search by reducing the computational complexity from O(N) to O(N), where N represents the size of the search space. This quantum algorithm leverages amplitude amplification to identify the correct solution significantly faster than classical linear search methods. The enhanced efficiency of Grover's algorithm fundamentally transforms search problems in unstructured databases by enabling fewer queries to the oracle function.
Quantum Speedup: How Grover Outperforms Classical Search
Grover's Algorithm achieves a quadratic speedup over classical brute-force search by reducing the search time from O(N) to O(N), significantly accelerating the process of finding a target item in an unsorted database. This quantum speedup is enabled through amplitude amplification and quantum superposition, allowing simultaneous evaluation of multiple possibilities. As a result, Grover's Algorithm outperforms classical search techniques, particularly in large datasets where classical methods become computationally expensive.
Space and Resource Requirements Comparison
Grover's Algorithm significantly reduces the number of required queries to O(N) compared to the O(N) queries in brute-force search, enabling faster search of unsorted databases. It demands additional quantum resources such as qubits and quantum gates, but overall space complexity remains more efficient due to fewer operations needed. Classical brute-force search consumes more memory and processing power as problem size grows, while Grover's algorithm leverages quantum parallelism, optimizing resource utilization for large search spaces.
Real-world Applications in Technology
Grover's Algorithm significantly accelerates unstructured database searches with a quadratic speedup over classical brute-force methods, reducing complexity from O(N) to O(N). This quantum advantage enables faster cryptographic key recovery, optimization problems, and large-scale data mining in technologies such as cybersecurity and machine learning. Real-world implementations leverage Grover's Algorithm to enhance search efficiency and tackle problems infeasible for classical computers.
Implementation Challenges and Limitations
Grover's Algorithm offers a quadratic speedup over brute-force search by efficiently locating unsorted database entries using quantum amplitude amplification, but its practical implementation faces significant challenges such as maintaining qubit coherence and error correction in noisy intermediate-scale quantum (NISQ) devices. The complexity of constructing oracle functions that accurately represent the search criteria limits scalability, while current hardware constraints restrict the algorithm's applicability to relatively small problem sizes compared to classical brute-force methods. These limitations illustrate the gap between theoretical advantages and real-world quantum computing capabilities, necessitating advancements in quantum hardware and algorithmic design for effective deployment.
Security Implications of Faster Search
Grover's Algorithm enables a quadratic speedup in searching unsorted databases, reducing the complexity from O(N) to O(N), which significantly impacts cryptographic security by making brute-force attacks more feasible against symmetric key algorithms. This acceleration challenges the effectiveness of traditional encryption methods like AES and necessitates longer key lengths or quantum-resistant algorithms to maintain security. As quantum computing progresses, relying on Grover's Algorithm in security assessments highlights the urgency for implementing post-quantum cryptography standards.
Future Prospects in Quantum Search Algorithms
Grover's Algorithm demonstrates a quadratic speedup over brute-force search by reducing search time from O(N) to O(N), making it a pivotal development in quantum search algorithms. Future prospects involve integrating Grover's principles with error-corrected quantum processors to tackle increasingly complex unstructured search problems. Advances in hybrid quantum-classical architectures are expected to further enhance search efficiency and scalability beyond current brute-force limitations.
Grover’s Algorithm vs Brute-force Search Infographic
 techiny.com
techiny.com