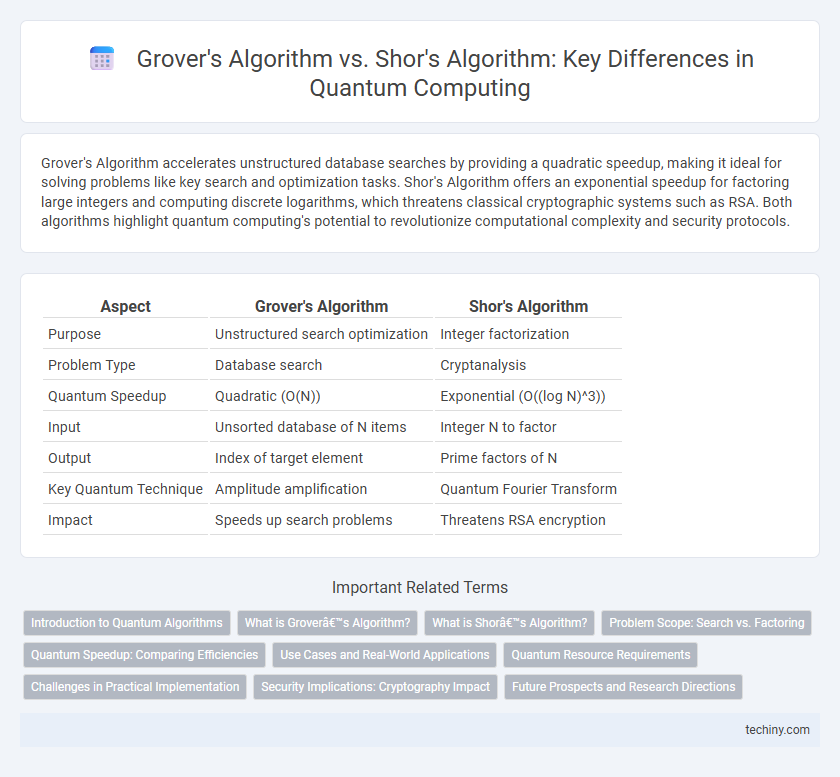
Grover's Algorithm accelerates unstructured database searches by providing a quadratic speedup, making it ideal for solving problems like key search and optimization tasks. Shor's Algorithm offers an exponential speedup for factoring large integers and computing discrete logarithms, which threatens classical cryptographic systems such as RSA. Both algorithms highlight quantum computing's potential to revolutionize computational complexity and security protocols.
Table of Comparison
| Aspect | Grover's Algorithm | Shor's Algorithm |
|---|---|---|
| Purpose | Unstructured search optimization | Integer factorization |
| Problem Type | Database search | Cryptanalysis |
| Quantum Speedup | Quadratic (O(N)) | Exponential (O((log N)^3)) |
| Input | Unsorted database of N items | Integer N to factor |
| Output | Index of target element | Prime factors of N |
| Key Quantum Technique | Amplitude amplification | Quantum Fourier Transform |
| Impact | Speeds up search problems | Threatens RSA encryption |
Introduction to Quantum Algorithms
Grover's algorithm offers a quadratic speedup for unstructured search problems, reducing the search complexity from O(N) to O(N) compared to classical algorithms. Shor's algorithm provides an exponential speedup in factoring large integers and computing discrete logarithms, solving problems that classical computers struggle with efficiently. Both algorithms highlight the potential of quantum computation to outperform classical methods in specific computational tasks by leveraging quantum superposition and entanglement.
What is Grover’s Algorithm?
Grover's Algorithm is a quantum search algorithm designed to find a specific item within an unsorted database of N elements in approximately N operations, providing a quadratic speedup over classical counterparts. It leverages quantum mechanics principles such as superposition and amplitude amplification to increase the probability of the desired outcome. Unlike Shor's Algorithm, which targets integer factorization, Grover's Algorithm is a general-purpose search algorithm applicable to a wide range of search problems.
What is Shor’s Algorithm?
Shor's Algorithm is a quantum algorithm designed for integer factorization, efficiently breaking down large numbers into their prime components exponentially faster than classical algorithms. It leverages quantum Fourier transform to solve problems related to discrete logarithms and factoring, which are foundational in cryptography. This algorithm poses a significant threat to widely used encryption methods such as RSA, reshaping the landscape of cybersecurity in quantum computing.
Problem Scope: Search vs. Factoring
Grover's Algorithm specializes in unstructured database search problems, offering a quadratic speedup by reducing the search time from O(N) to O(N), which is particularly useful for verifying or finding a desired item within an unsorted dataset. Shor's Algorithm targets integer factorization and discrete logarithms, a problem critical to cryptography, achieving exponential speedup over classical algorithms by solving these problems in polynomial time. The fundamental difference lies in Grover's suitability for general search challenges, while Shor's addresses specific mathematical problems that underpin modern encryption systems.
Quantum Speedup: Comparing Efficiencies
Grover's algorithm delivers quadratic speedup for unstructured search problems, reducing the complexity from O(N) in classical algorithms to O(N) on a quantum computer. Shor's algorithm achieves exponential speedup in factoring large integers, transforming a classical sub-exponential time complexity into polynomial time with respect to the number of digits. These distinct efficiencies highlight Grover's relevance in database searching and Shor's critical impact on cryptography by efficiently solving integer factorization.
Use Cases and Real-World Applications
Grover's Algorithm excels in unstructured search problems, significantly speeding up database queries and optimization tasks in cryptography and machine learning. Shor's Algorithm is specifically designed for integer factorization, posing a direct threat to classical encryption methods such as RSA by efficiently breaking large prime-based cryptographic keys. Real-world applications of Grover's Algorithm include database search and combinatorial optimization, while Shor's Algorithm is pivotal in quantum cryptanalysis and securing communications against quantum attacks.
Quantum Resource Requirements
Grover's Algorithm requires O(N) quantum operations and utilizes fewer qubits, making it suitable for unstructured search problems on near-term quantum devices. Shor's Algorithm demands exponentially more quantum resources, including a large number of qubits and deep quantum circuits, to efficiently factor large integers. The quantum resource intensity of Shor's Algorithm limits its current practical implementation compared to the relatively resource-efficient Grover's Algorithm.
Challenges in Practical Implementation
Grover's Algorithm faces challenges in practical implementation due to its requirement for a large number of quantum gates and error correction to maintain coherence during database search tasks. Shor's Algorithm encounters difficulties primarily with qubit scalability and error rates when factoring large integers, demanding highly stable qubits and fault-tolerant quantum circuits. Both algorithms necessitate advancements in qubit stability, error correction protocols, and quantum hardware to be effectively realized in practical scenarios.
Security Implications: Cryptography Impact
Grover's Algorithm significantly reduces the complexity of unstructured search problems, enabling attacks on symmetric key cryptography by effectively halving the security level of algorithms like AES. Shor's Algorithm, by efficiently factoring large integers and computing discrete logarithms, directly threatens public-key cryptosystems such as RSA and ECC, rendering them vulnerable to quantum attacks. The contrasting impacts highlight urgent needs for quantum-resistant cryptographic standards to secure data against both symmetric and asymmetric algorithm breaches.
Future Prospects and Research Directions
Grover's Algorithm and Shor's Algorithm represent pivotal advancements in quantum computing with distinct future research paths; Grover's Algorithm focuses on optimization problems and unstructured search improvements, while Shor's Algorithm drives progress in integer factorization and cryptanalysis. Emerging quantum hardware developments and error-correction techniques aim to enhance the practical implementation of both algorithms, propelling advancements in quantum cryptography and secure communications. Research directions emphasize hybrid quantum-classical methods, algorithmic scalability, and exploring new quantum algorithms to extend the capabilities of quantum computation beyond current limitations.
Grover’s Algorithm vs Shor’s Algorithm Infographic
 techiny.com
techiny.com