Entropy measures the uncertainty or disorder within a dataset, quantifying the impurity of a collection of examples. Information gain calculates the reduction in entropy achieved by splitting the dataset based on a specific attribute, guiding the selection of the most informative features for model building. Maximizing information gain helps optimize decision trees by creating branches that produce the most homogenous subsets, enhancing predictive accuracy.
Table of Comparison
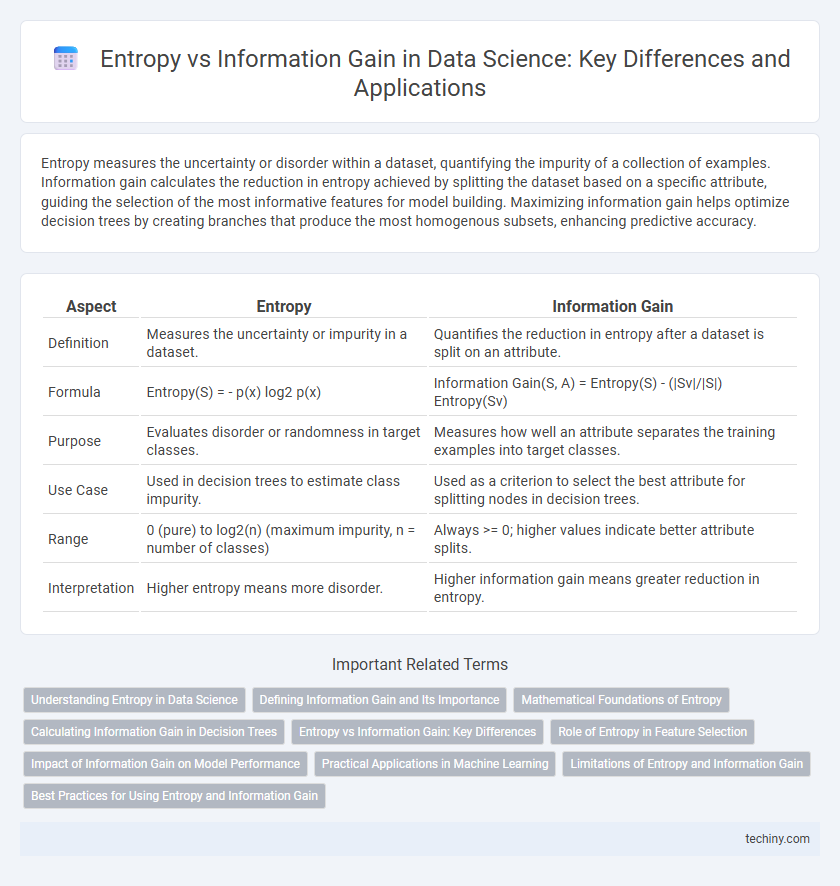
| Aspect | Entropy | Information Gain |
|---|---|---|
| Definition | Measures the uncertainty or impurity in a dataset. | Quantifies the reduction in entropy after a dataset is split on an attribute. |
| Formula | Entropy(S) = - p(x) log2 p(x) | Information Gain(S, A) = Entropy(S) - (|Sv|/|S|) Entropy(Sv) |
| Purpose | Evaluates disorder or randomness in target classes. | Measures how well an attribute separates the training examples into target classes. |
| Use Case | Used in decision trees to estimate class impurity. | Used as a criterion to select the best attribute for splitting nodes in decision trees. |
| Range | 0 (pure) to log2(n) (maximum impurity, n = number of classes) | Always >= 0; higher values indicate better attribute splits. |
| Interpretation | Higher entropy means more disorder. | Higher information gain means greater reduction in entropy. |
Understanding Entropy in Data Science
Entropy in data science quantifies the uncertainty or impurity within a dataset, measuring the disorder in class distribution. A high entropy value indicates a diverse and mixed dataset, while a low entropy signals more homogeneous or pure data subsets. Understanding entropy is crucial for algorithms like decision trees, where minimizing entropy leads to effective information gain and improved model accuracy.
Defining Information Gain and Its Importance
Information gain quantifies the reduction in entropy or uncertainty in a dataset after a split based on a particular attribute, making it a crucial metric in decision tree algorithms. By measuring how well an attribute separates the training examples according to their target classification, information gain guides the selection of features that maximize the predictability of the model. This optimization enhances the accuracy and efficiency of classification tasks in supervised learning.
Mathematical Foundations of Entropy
Entropy quantifies the uncertainty or impurity in a dataset, calculated using the probability distribution of classes with the formula \( H(S) = -\sum p_i \log_2 p_i \). Information gain measures the reduction in entropy after a dataset is split on an attribute, guiding decision tree algorithms to select the most informative features. Understanding these mathematical foundations is crucial for optimizing feature selection and improving model accuracy in classification tasks.
Calculating Information Gain in Decision Trees
Information Gain in decision trees quantifies the reduction in entropy after a dataset is split based on a particular attribute, guiding the selection of the most informative features. It is calculated by subtracting the weighted entropy of the child nodes from the entropy of the parent node, effectively measuring the purity improvement achieved by the split. Higher Information Gain values indicate attributes that best partition the data, enhancing the accuracy of the classification model.
Entropy vs Information Gain: Key Differences
Entropy measures the uncertainty or disorder within a dataset by quantifying the amount of randomness in class labels. Information gain evaluates the reduction in entropy after splitting a dataset based on an attribute, indicating how well an attribute separates the classes. The key difference lies in entropy representing the impurity of a dataset, while information gain measures the effectiveness of an attribute in improving the classification.
Role of Entropy in Feature Selection
Entropy quantifies the uncertainty or impurity in a dataset, serving as a fundamental metric for evaluating the randomness within class distributions. In feature selection, entropy measures the disorder before and after splitting data based on a feature, helping to identify attributes that provide the most informative partitions. By calculating the reduction in entropy, known as information gain, data scientists can prioritize features that maximize the clarity and predictive power of machine learning models.
Impact of Information Gain on Model Performance
Information gain measures the reduction in entropy after a dataset split, directly influencing decision tree accuracy by selecting features that maximize this measure. Higher information gain leads to purer child nodes, improving model interpretability and predictive performance. Optimizing splits based on information gain enhances the tree's ability to generalize from training data to unseen instances.
Practical Applications in Machine Learning
Entropy quantifies the impurity or uncertainty within a dataset, serving as a foundational metric in decision tree algorithms like ID3 and C4.5 for feature selection. Information gain measures the reduction in entropy after a dataset is split on a specific attribute, guiding the model to choose the most informative features that improve classification accuracy. These concepts enhance model interpretability and efficiency by systematically reducing uncertainty and optimizing the decision-making process in supervised learning tasks.
Limitations of Entropy and Information Gain
Entropy can be biased toward attributes with many distinct values, leading to overfitting and less generalizable models. Information Gain, relying on entropy, inherits this drawback and may favor splits with numerous branches rather than those most predictive of the target variable. Both measures struggle with handling continuous variables and noise without proper discretization or preprocessing, limiting their effectiveness in complex datasets.
Best Practices for Using Entropy and Information Gain
Optimal use of entropy and information gain in data science involves carefully selecting features that maximize information gain to improve model accuracy while minimizing overfitting. Calculating entropy accurately helps quantify the impurity within datasets, guiding decision tree algorithms to make more informed splits. Employing techniques such as pruning and cross-validation complements the use of entropy and information gain by enhancing generalization and reducing noise sensitivity.
entropy vs information gain Infographic
 techiny.com
techiny.com