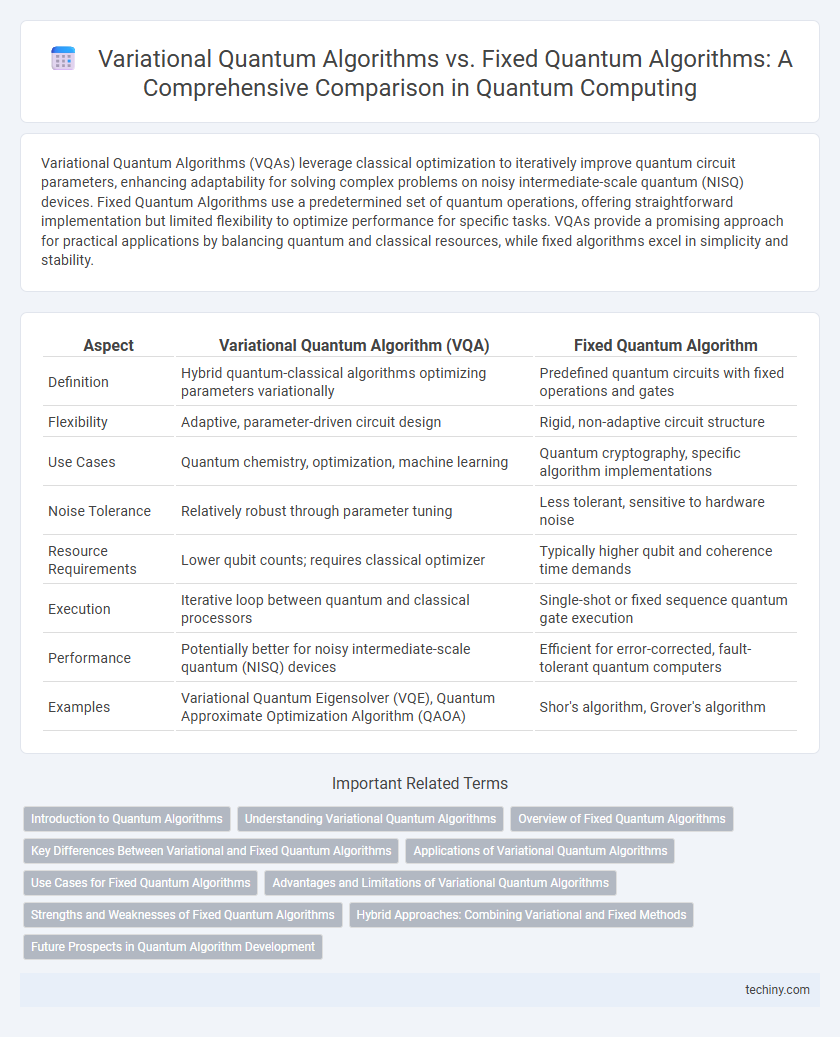
Variational Quantum Algorithms (VQAs) leverage classical optimization to iteratively improve quantum circuit parameters, enhancing adaptability for solving complex problems on noisy intermediate-scale quantum (NISQ) devices. Fixed Quantum Algorithms use a predetermined set of quantum operations, offering straightforward implementation but limited flexibility to optimize performance for specific tasks. VQAs provide a promising approach for practical applications by balancing quantum and classical resources, while fixed algorithms excel in simplicity and stability.
Table of Comparison
| Aspect | Variational Quantum Algorithm (VQA) | Fixed Quantum Algorithm |
|---|---|---|
| Definition | Hybrid quantum-classical algorithms optimizing parameters variationally | Predefined quantum circuits with fixed operations and gates |
| Flexibility | Adaptive, parameter-driven circuit design | Rigid, non-adaptive circuit structure |
| Use Cases | Quantum chemistry, optimization, machine learning | Quantum cryptography, specific algorithm implementations |
| Noise Tolerance | Relatively robust through parameter tuning | Less tolerant, sensitive to hardware noise |
| Resource Requirements | Lower qubit counts; requires classical optimizer | Typically higher qubit and coherence time demands |
| Execution | Iterative loop between quantum and classical processors | Single-shot or fixed sequence quantum gate execution |
| Performance | Potentially better for noisy intermediate-scale quantum (NISQ) devices | Efficient for error-corrected, fault-tolerant quantum computers |
| Examples | Variational Quantum Eigensolver (VQE), Quantum Approximate Optimization Algorithm (QAOA) | Shor's algorithm, Grover's algorithm |
Introduction to Quantum Algorithms
Variational Quantum Algorithms leverage parameterized quantum circuits optimized through classical feedback loops, offering adaptability to complex problems and noise resilience in near-term quantum devices. Fixed Quantum Algorithms utilize predetermined quantum circuits with specific gate sequences designed for particular tasks like Shor's or Grover's algorithms, providing guaranteed outcomes on ideal quantum hardware but limited flexibility. Understanding their fundamental differences is crucial for selecting appropriate quantum computing strategies in algorithm development and implementation.
Understanding Variational Quantum Algorithms
Variational Quantum Algorithms (VQAs) leverage parameterized quantum circuits optimized through classical feedback loops to solve complex problems, offering adaptability that fixed quantum algorithms lack. VQAs excel in near-term quantum devices, mitigating noise and hardware limitations by iteratively refining parameters to minimize a cost function, such as in the Variational Quantum Eigensolver (VQE). This approach enables efficient approximate solutions for chemistry, optimization, and machine learning tasks, harnessing quantum-classical hybrid computations.
Overview of Fixed Quantum Algorithms
Fixed quantum algorithms rely on predetermined quantum circuits designed to solve specific problems without adaptive parameter tuning. Notable examples include Shor's algorithm for integer factorization and Grover's algorithm for unstructured search, both demonstrating exponential speedups over classical counterparts. These algorithms emphasize rigidity in structure, contrasting with the flexibility seen in variational quantum algorithms that optimize parameters dynamically through classical-quantum feedback loops.
Key Differences Between Variational and Fixed Quantum Algorithms
Variational Quantum Algorithms (VQAs) leverage parameterized quantum circuits optimized through classical feedback loops, enabling adaptability and mitigation of quantum noise, whereas Fixed Quantum Algorithms utilize pre-defined circuits with fixed gates designed for specific tasks without iterative optimization. VQAs are particularly suited for near-term noisy intermediate-scale quantum (NISQ) devices due to their flexibility and error resilience, while Fixed Quantum Algorithms often require fault-tolerant quantum hardware for reliable implementation. The core distinction lies in the hybrid quantum-classical approach of VQAs versus the purely quantum, deterministic nature of Fixed Quantum Algorithms.
Applications of Variational Quantum Algorithms
Variational Quantum Algorithms (VQAs) excel in solving complex optimization problems, quantum chemistry simulations, and machine learning tasks by leveraging parameterized quantum circuits optimized via classical feedback loops. Unlike Fixed Quantum Algorithms, which rely on predetermined gate sequences, VQAs adapt dynamically to problem-specific landscapes, enabling efficient resource use on near-term quantum hardware. Their hybrid quantum-classical framework significantly accelerates solutions for combinatorial optimization and electronic structure calculations in practical quantum computing applications.
Use Cases for Fixed Quantum Algorithms
Fixed quantum algorithms excel in specific, well-defined tasks such as factoring large integers with Shor's algorithm and unstructured database search via Grover's algorithm, providing proven quantum speedups. These algorithms are highly efficient for problems with known quantum circuits and fixed structures, enabling practical implementations on near-term quantum hardware. Use cases include cryptanalysis, quantum chemistry simulations with fixed Hamiltonians, and certain optimization problems where the algorithm's parameters do not require adaptation.
Advantages and Limitations of Variational Quantum Algorithms
Variational Quantum Algorithms (VQAs) offer flexibility and error mitigation by combining classical optimization with quantum circuit evaluations, making them well-suited for near-term quantum devices with limited qubit counts and coherence times. Their adaptive nature allows tackling complex problems like quantum chemistry and combinatorial optimization, but they face challenges such as barren plateaus and sensitivity to noise, which can hinder convergence and scalability. Unlike fixed quantum algorithms, VQAs require careful parameter tuning and may not guarantee polynomial-time solutions, limiting their applicability to certain problem domains.
Strengths and Weaknesses of Fixed Quantum Algorithms
Fixed quantum algorithms, such as Shor's and Grover's algorithms, excel in solving specific computational problems with proven exponential or quadratic speedups over classical counterparts. Their rigidity ensures predictable performance and well-understood error characteristics, making them robust for well-defined tasks like factorization and unstructured search. However, their lack of adaptability to varying problem instances limits their applicability across a broader range of quantum applications compared to the flexible parameterization found in variational quantum algorithms.
Hybrid Approaches: Combining Variational and Fixed Methods
Hybrid approaches in quantum computing leverage the strengths of both variational quantum algorithms (VQAs) and fixed quantum algorithms by integrating parameterized quantum circuits with predetermined quantum routines. These methods optimize quantum resources by using classical feedback loops to adapt variational components while maintaining the stability and predictability of fixed subroutines. Combining VQAs with fixed algorithms enhances problem-solving robustness and scalability, particularly in noisy intermediate-scale quantum (NISQ) devices where error mitigation and resource efficiency are critical.
Future Prospects in Quantum Algorithm Development
Variational Quantum Algorithms (VQAs) offer promising scalability and adaptability advantages compared to Fixed Quantum Algorithms, making them prime candidates for near-term quantum devices with limited qubit counts and noisy environments. Research into hybrid quantum-classical optimization methods intrinsic to VQAs continues to advance their application in quantum chemistry, material science, and machine learning. Emerging developments in error mitigation and algorithmic resilience will likely position VQAs as foundational tools in the evolving landscape of quantum algorithm development.
Variational Quantum Algorithm vs Fixed Quantum Algorithm Infographic
 techiny.com
techiny.com