Autoencoders and PCA both reduce data dimensionality but differ in approach and complexity. Autoencoders use neural networks to capture nonlinear patterns, making them suitable for complex data, while PCA relies on linear transformations to project data onto principal components. Choosing between them depends on data complexity and the need for capturing nonlinear relationships in feature extraction.
Table of Comparison
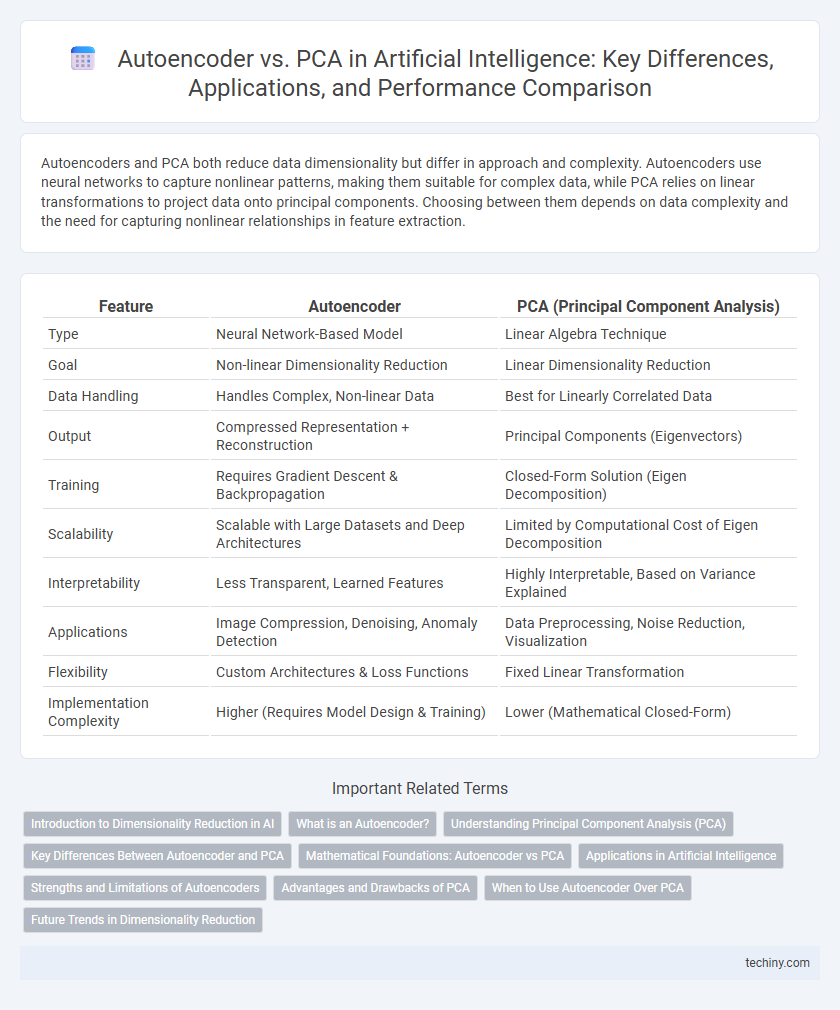
| Feature | Autoencoder | PCA (Principal Component Analysis) |
|---|---|---|
| Type | Neural Network-Based Model | Linear Algebra Technique |
| Goal | Non-linear Dimensionality Reduction | Linear Dimensionality Reduction |
| Data Handling | Handles Complex, Non-linear Data | Best for Linearly Correlated Data |
| Output | Compressed Representation + Reconstruction | Principal Components (Eigenvectors) |
| Training | Requires Gradient Descent & Backpropagation | Closed-Form Solution (Eigen Decomposition) |
| Scalability | Scalable with Large Datasets and Deep Architectures | Limited by Computational Cost of Eigen Decomposition |
| Interpretability | Less Transparent, Learned Features | Highly Interpretable, Based on Variance Explained |
| Applications | Image Compression, Denoising, Anomaly Detection | Data Preprocessing, Noise Reduction, Visualization |
| Flexibility | Custom Architectures & Loss Functions | Fixed Linear Transformation |
| Implementation Complexity | Higher (Requires Model Design & Training) | Lower (Mathematical Closed-Form) |
Introduction to Dimensionality Reduction in AI
Dimensionality reduction techniques like Autoencoders and Principal Component Analysis (PCA) play a critical role in processing high-dimensional data in Artificial Intelligence. Autoencoders leverage neural networks to learn non-linear data representations, enabling the capture of complex patterns beyond linear correlations that PCA relies on. PCA reduces dimensionality by transforming data into orthogonal components ranked by variance, making it suitable for linearly separable datasets but less effective for intricate feature extraction compared to Autoencoders.
What is an Autoencoder?
An autoencoder is a type of artificial neural network designed to learn efficient data representations through unsupervised learning by encoding input data into a lower-dimensional latent space and reconstructing it back to the original form. Unlike PCA, which is a linear dimensionality reduction technique, autoencoders can capture complex, nonlinear relationships in data using multiple hidden layers and nonlinear activation functions. This capability makes autoencoders highly effective for tasks such as image compression, denoising, and anomaly detection in artificial intelligence applications.
Understanding Principal Component Analysis (PCA)
Principal Component Analysis (PCA) is a statistical technique that reduces the dimensionality of data by identifying the directions (principal components) where the variance is maximized. Unlike autoencoders, which use neural networks to learn efficient codings of input data, PCA linearly transforms data by projecting it onto orthogonal components. This method captures the most significant features in the data, facilitating noise reduction and feature extraction in machine learning tasks.
Key Differences Between Autoencoder and PCA
Autoencoders and Principal Component Analysis (PCA) are both dimensionality reduction techniques, but autoencoders use neural networks to learn nonlinear representations, while PCA relies on linear transformations. Autoencoders can capture complex data structures through multiple layers and nonlinear activation functions, enabling better reconstruction for high-dimensional and non-linear data. PCA, on the other hand, excels in simplicity and interpretability by projecting data onto orthogonal principal components but is limited to linear relationships.
Mathematical Foundations: Autoencoder vs PCA
Autoencoders leverage nonlinear transformations through neural networks to capture complex data distributions, minimizing reconstruction loss with backpropagation. Principal Component Analysis (PCA) uses linear algebra to compute orthogonal eigenvectors of the covariance matrix, projecting data onto lower-dimensional subspaces with maximal variance. While PCA relies on spectral decomposition and is limited to linear correlations, autoencoders can model intricate nonlinear relationships due to their layered architecture and activation functions.
Applications in Artificial Intelligence
Autoencoders offer nonlinear dimensionality reduction, making them ideal for complex data representation in artificial intelligence tasks like image reconstruction, anomaly detection, and feature extraction in deep learning models. Principal Component Analysis (PCA) provides a linear approach to reduce dimensionality, commonly used for simplifying datasets, enhancing visualization, and pre-processing steps in machine learning algorithms. Autoencoders outperform PCA in capturing intricate data patterns, supporting advanced AI applications such as natural language processing and generative modeling.
Strengths and Limitations of Autoencoders
Autoencoders excel in capturing complex nonlinear patterns in high-dimensional data, making them powerful for feature extraction and dimensionality reduction beyond the linear capabilities of PCA. Their flexibility allows customization through deep neural network architectures, enabling improved reconstruction quality and handling of diverse data types like images and text. However, autoencoders require large datasets and significant computational resources for training, and they are prone to overfitting without proper regularization or architectural constraints.
Advantages and Drawbacks of PCA
PCA (Principal Component Analysis) offers a straightforward mathematical approach for dimensionality reduction by identifying linear combinations of features that maximize variance, making it computationally efficient and interpretable. However, PCA struggles with capturing non-linear relationships in complex datasets, limiting its effectiveness for high-dimensional data with intricate structures. Compared to autoencoders, PCA's reliance on linearity and covariance-based transformations reduces flexibility but ensures faster training and easier visualization of principal components.
When to Use Autoencoder Over PCA
Autoencoders are preferred over PCA when dealing with nonlinear dimensionality reduction since they can capture complex, non-linear patterns in high-dimensional data through deep neural networks. They excel in scenarios requiring feature learning for tasks like image compression, denoising, or anomaly detection where traditional linear methods like PCA fall short. Autoencoders also outperform PCA when working with large-scale datasets that benefit from scalable, customizable architectures.
Future Trends in Dimensionality Reduction
Future trends in dimensionality reduction emphasize the growing integration of autoencoders with deep learning architectures, leveraging their ability to capture complex, nonlinear data patterns beyond traditional PCA's linear transformations. Advances in variational autoencoders and generative models are pushing the boundaries of feature extraction, enabling more efficient representations in high-dimensional spaces for applications like image recognition and natural language processing. The convergence of neural networks with probabilistic methods signals a shift towards adaptive, scalable dimensionality reduction techniques that maintain interpretability while maximizing data compression.
Autoencoder vs PCA Infographic
 techiny.com
techiny.com