Gradient descent optimizes models by iteratively adjusting parameters to minimize a loss function, making it highly efficient for differentiable problems in machine learning. Evolutionary algorithms simulate natural selection processes, exploring diverse solution spaces without requiring gradient information, which is advantageous for complex, multimodal, or non-differentiable optimization tasks. Both methods offer unique strengths, with gradient descent excelling in speed and precision, while evolutionary algorithms provide robustness in global search and adaptability.
Table of Comparison
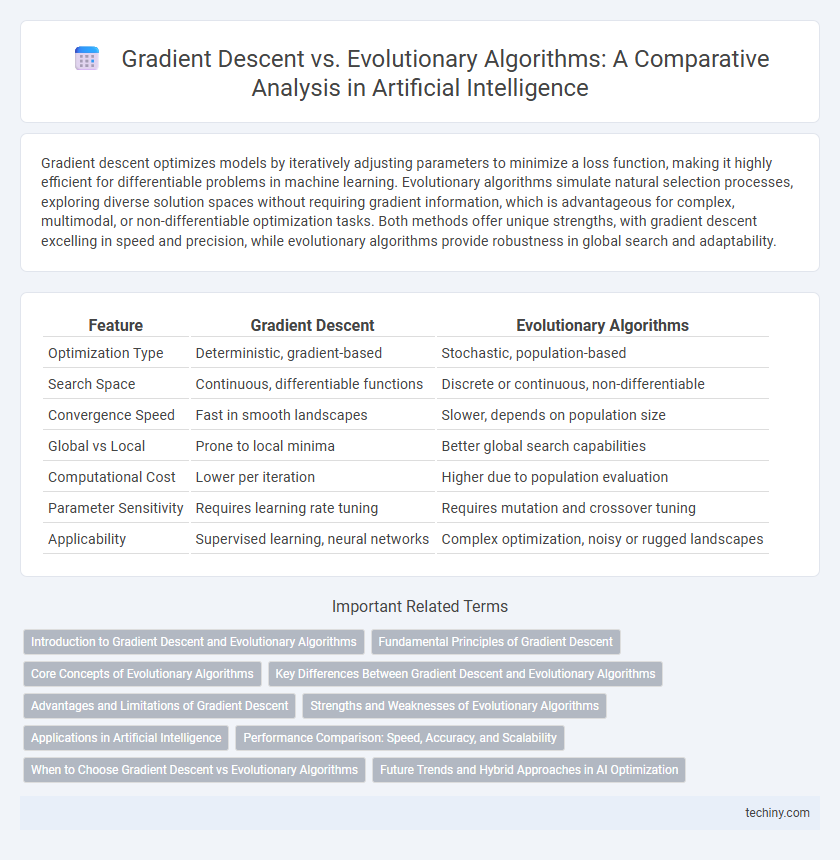
| Feature | Gradient Descent | Evolutionary Algorithms |
|---|---|---|
| Optimization Type | Deterministic, gradient-based | Stochastic, population-based |
| Search Space | Continuous, differentiable functions | Discrete or continuous, non-differentiable |
| Convergence Speed | Fast in smooth landscapes | Slower, depends on population size |
| Global vs Local | Prone to local minima | Better global search capabilities |
| Computational Cost | Lower per iteration | Higher due to population evaluation |
| Parameter Sensitivity | Requires learning rate tuning | Requires mutation and crossover tuning |
| Applicability | Supervised learning, neural networks | Complex optimization, noisy or rugged landscapes |
Introduction to Gradient Descent and Evolutionary Algorithms
Gradient Descent is an optimization algorithm widely used in machine learning for minimizing loss functions by iteratively adjusting parameters in the direction of the steepest descent. Evolutionary Algorithms are inspired by natural selection processes, employing mechanisms such as mutation, crossover, and selection to evolve solutions across generations. Both techniques serve as fundamental methods for solving complex optimization problems within artificial intelligence, with Gradient Descent excelling in continuous domains and Evolutionary Algorithms offering robustness in multimodal and discrete search spaces.
Fundamental Principles of Gradient Descent
Gradient descent is an optimization algorithm that iteratively adjusts parameters to minimize a cost function by moving in the direction of the steepest negative gradient. It relies on continuous differentiability of the objective function and calculates gradients using techniques such as backpropagation in neural networks. This method efficiently converges to local minima by leveraging gradient information, making it fundamental in training deep learning models.
Core Concepts of Evolutionary Algorithms
Evolutionary algorithms mimic natural selection by iteratively selecting, mutating, and recombining candidate solutions to optimize complex problems. These algorithms rely on population-based search, fitness evaluation, and genetic operators to explore large, nonlinear solution spaces without requiring gradient information. Unlike gradient descent, evolutionary algorithms excel in handling multimodal, discontinuous, and noisy optimization landscapes due to their stochastic and derivative-free nature.
Key Differences Between Gradient Descent and Evolutionary Algorithms
Gradient Descent optimizes differentiable functions by iteratively updating parameters based on the gradient, ensuring efficient convergence for convex problems. Evolutionary Algorithms rely on population-based stochastic search mechanisms inspired by natural selection, excelling in multi-modal, non-differentiable, or complex landscapes where gradients are unavailable. Key differences include Gradient Descent's deterministic nature and reliance on gradient information versus the stochastic, gradient-free search strategy of Evolutionary Algorithms.
Advantages and Limitations of Gradient Descent
Gradient descent excels in optimizing differentiable functions due to its efficient convergence and scalability in high-dimensional parameter spaces, making it ideal for training deep neural networks. Its limitations include susceptibility to local minima, sensitivity to learning rate selection, and poor performance on non-differentiable or highly non-convex objective functions. Gradient descent also requires gradient information, which restricts its applicability in problems where the objective function is unknown or noisy, in contrast to the population-based search of evolutionary algorithms.
Strengths and Weaknesses of Evolutionary Algorithms
Evolutionary Algorithms excel in exploring large, complex search spaces without requiring gradient information, making them suitable for optimization problems with discontinuous or noisy objective functions. Their population-based approach ensures robustness against local minima but often results in slower convergence compared to gradient-based methods. However, they can be computationally expensive and less efficient for high-dimensional problems where gradient descent methods perform better.
Applications in Artificial Intelligence
Gradient descent excels in optimizing deep learning models by efficiently minimizing loss functions through iterative parameter updates, making it ideal for training neural networks in image recognition and natural language processing. Evolutionary algorithms offer robust solutions for optimization problems with complex, multimodal landscapes or discrete variables, finding applications in AI-driven game strategies, robotic control, and symbolic regression. Combining gradient descent's precision with evolutionary algorithms' global search capabilities enhances AI systems' adaptability and performance in dynamic environments.
Performance Comparison: Speed, Accuracy, and Scalability
Gradient descent typically offers faster convergence on smooth, differentiable objective functions due to its use of precise gradient information, making it highly efficient for large-scale machine learning models. Evolutionary algorithms, while generally slower and computationally intensive, excel in global optimization and avoid local minima, providing higher accuracy in complex, multimodal search spaces. Scalability favors gradient descent in deep learning tasks, whereas evolutionary algorithms require significant computational resources as problem dimensionality increases, limiting their practicality for large-scale applications.
When to Choose Gradient Descent vs Evolutionary Algorithms
Gradient Descent is ideal for optimizing differentiable functions with large datasets and smooth cost surfaces, making it the preferred choice in deep learning and neural network training. Evolutionary Algorithms excel in complex, multimodal, or discrete optimization problems where gradient information is unavailable or unreliable, such as combinatorial optimization and design optimization tasks. Choosing between these methods depends on problem structure, availability of gradient data, and convergence speed requirements.
Future Trends and Hybrid Approaches in AI Optimization
Future trends in AI optimization emphasize hybrid approaches combining gradient descent and evolutionary algorithms to leverage the strengths of both techniques. Gradient descent offers efficient convergence in differentiable landscapes, while evolutionary algorithms excel in exploring complex, multimodal search spaces without gradient information. Integrating these methods enables robust optimization, adaptive learning rates, and improved performance in dynamic environments, advancing AI capabilities across diverse applications.
Gradient Descent vs Evolutionary Algorithms Infographic
 techiny.com
techiny.com