Monte Carlo Simulation uses random sampling to model complex systems and assess the impact of uncertainty on outcomes, particularly effective in scenarios with defined probabilistic models. Bootstrapping resamples data with replacement to estimate the sampling distribution and infer statistical properties, excelling in situations with limited or unknown population parameters. Both methods provide powerful tools for uncertainty quantification but differ fundamentally in approach and application within data science.
Table of Comparison
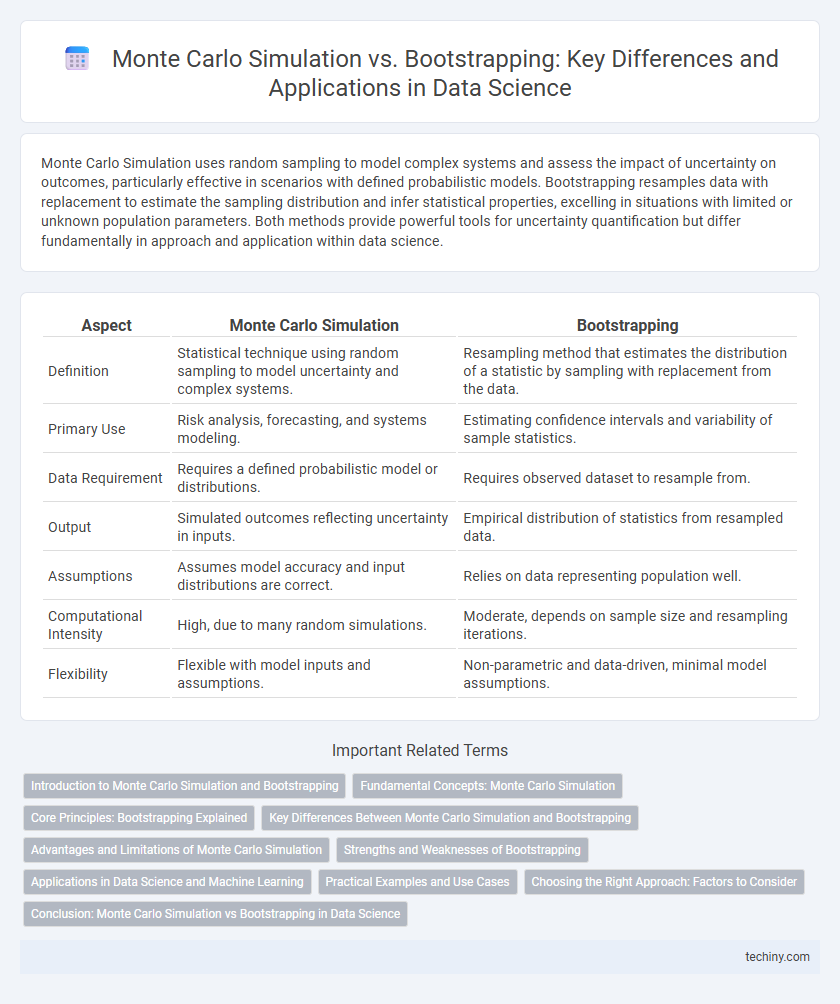
| Aspect | Monte Carlo Simulation | Bootstrapping |
|---|---|---|
| Definition | Statistical technique using random sampling to model uncertainty and complex systems. | Resampling method that estimates the distribution of a statistic by sampling with replacement from the data. |
| Primary Use | Risk analysis, forecasting, and systems modeling. | Estimating confidence intervals and variability of sample statistics. |
| Data Requirement | Requires a defined probabilistic model or distributions. | Requires observed dataset to resample from. |
| Output | Simulated outcomes reflecting uncertainty in inputs. | Empirical distribution of statistics from resampled data. |
| Assumptions | Assumes model accuracy and input distributions are correct. | Relies on data representing population well. |
| Computational Intensity | High, due to many random simulations. | Moderate, depends on sample size and resampling iterations. |
| Flexibility | Flexible with model inputs and assumptions. | Non-parametric and data-driven, minimal model assumptions. |
Introduction to Monte Carlo Simulation and Bootstrapping
Monte Carlo Simulation uses repeated random sampling to model the probability of different outcomes in processes that are inherently uncertain, providing a robust framework for risk assessment and decision-making. Bootstrapping is a resampling technique that generates multiple datasets from a single sample by sampling with replacement, enabling precise estimation of statistics such as confidence intervals and standard errors without relying on parametric assumptions. Both methods are essential in data science for quantifying uncertainty and enhancing the reliability of predictive models through empirical data analysis.
Fundamental Concepts: Monte Carlo Simulation
Monte Carlo Simulation is a statistical technique that uses random sampling and repeated computations to model complex systems and estimate the probability distribution of uncertain outcomes. It relies on generating large numbers of random variables to simulate the behavior of a system under various scenarios, enabling the quantification of risk and uncertainty. This approach is widely applied in data science for optimizing algorithms, financial modeling, and risk assessment by approximating solutions to problems that are analytically intractable.
Core Principles: Bootstrapping Explained
Bootstrapping is a resampling technique in data science that involves repeatedly drawing samples with replacement from an original dataset to estimate the sampling distribution of a statistic. This non-parametric method allows for the approximation of confidence intervals and standard errors without relying on strict assumptions about the underlying population distribution. Unlike Monte Carlo simulation, which generates data based on a specified probabilistic model, bootstrapping directly leverages the observed data to assess variability and uncertainty in statistical estimates.
Key Differences Between Monte Carlo Simulation and Bootstrapping
Monte Carlo Simulation relies on generating random samples from a known probability distribution to model complex systems and estimate outcomes, while Bootstrapping resamples with replacement directly from observed data to assess the variability of a statistic. Monte Carlo is primarily used when the underlying distribution is specified or assumed, making it ideal for risk assessment and probabilistic modeling, whereas Bootstrapping is non-parametric and ideal for estimating confidence intervals and standard errors without assuming a specific distribution. The key difference lies in Monte Carlo's dependence on theoretical distributions versus Bootstrapping's emphasis on empirical data resampling for inferential statistics.
Advantages and Limitations of Monte Carlo Simulation
Monte Carlo Simulation excels in handling complex probabilistic models and uncertainty quantification by generating a large number of random samples to approximate distributions. Its advantages include flexibility in modeling diverse scenarios and scalability for high-dimensional problems. However, limitations involve high computational cost for simulating extensive datasets and potential inaccuracies if the input distributions are poorly specified.
Strengths and Weaknesses of Bootstrapping
Bootstrapping excels in estimating the sampling distribution without relying on strict parametric assumptions, making it highly flexible for small or complex datasets. Its main weakness lies in its dependency on the original sample, which may introduce bias if the sample is not representative or contains outliers. Unlike Monte Carlo Simulation, bootstrapping can struggle with computational intensity when applied to very large datasets or highly complex models.
Applications in Data Science and Machine Learning
Monte Carlo Simulation is widely used in data science for risk assessment, probabilistic modeling, and optimization problems where complex systems require stochastic input variables. Bootstrapping serves as a powerful resampling technique to estimate the accuracy of sample statistics, improve model validation, and enhance confidence intervals in machine learning applications. Both methods contribute significantly to uncertainty quantification but differ in their approach, with Monte Carlo relying on repeated random sampling from predefined distributions and Bootstrapping drawing samples from the empirical data itself.
Practical Examples and Use Cases
Monte Carlo Simulation generates random samples from specified probability distributions to model complex systems, widely used in financial risk assessment and portfolio optimization. Bootstrapping resamples observed data to estimate the sampling distribution, often applied in hypothesis testing and confidence interval construction for small datasets. Practical use cases include Monte Carlo for predicting stock price movements and Bootstrapping for estimating model accuracy in machine learning algorithms.
Choosing the Right Approach: Factors to Consider
Choosing between Monte Carlo Simulation and Bootstrapping depends on the nature of the data and the specific problem. Monte Carlo Simulation excels in modeling complex systems with known probabilistic models, while Bootstrapping is ideal for estimating the sampling distribution of statistics from limited empirical data. Consider data availability, computational resources, and the underlying assumptions to select the most appropriate method for accurate and reliable inferential results.
Conclusion: Monte Carlo Simulation vs Bootstrapping in Data Science
Monte Carlo Simulation offers robust modeling of complex probabilistic systems through repeated random sampling, making it ideal for scenarios requiring estimation of uncertain outcomes based on known probability distributions. Bootstrapping excels in assessing the variability and confidence intervals of statistical estimates by resampling observed data without assuming an underlying distribution, enhancing inferential accuracy in smaller datasets. Selecting between Monte Carlo Simulation and Bootstrapping depends on the availability of theoretical distribution models and the need for empirical data-driven inference in data science applications.
Monte Carlo Simulation vs Bootstrapping Infographic
 techiny.com
techiny.com