Time series forecasting analyzes data points collected or recorded at specific time intervals to predict future trends, making it essential for understanding patterns over time. Cross-sectional analysis examines data collected from multiple subjects at a single point in time, ideal for identifying differences and relationships among variables. Both techniques provide complementary insights, with time series focusing on temporal dynamics and cross-sectional analysis emphasizing variation across entities.
Table of Comparison
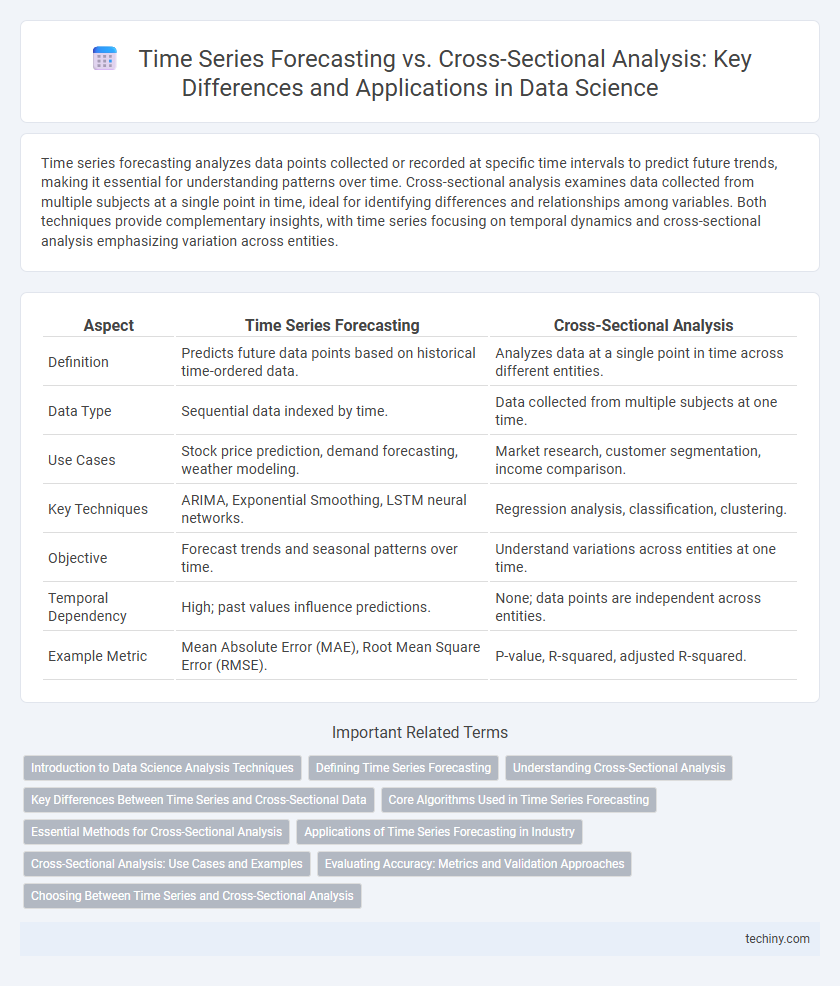
| Aspect | Time Series Forecasting | Cross-Sectional Analysis |
|---|---|---|
| Definition | Predicts future data points based on historical time-ordered data. | Analyzes data at a single point in time across different entities. |
| Data Type | Sequential data indexed by time. | Data collected from multiple subjects at one time. |
| Use Cases | Stock price prediction, demand forecasting, weather modeling. | Market research, customer segmentation, income comparison. |
| Key Techniques | ARIMA, Exponential Smoothing, LSTM neural networks. | Regression analysis, classification, clustering. |
| Objective | Forecast trends and seasonal patterns over time. | Understand variations across entities at one time. |
| Temporal Dependency | High; past values influence predictions. | None; data points are independent across entities. |
| Example Metric | Mean Absolute Error (MAE), Root Mean Square Error (RMSE). | P-value, R-squared, adjusted R-squared. |
Introduction to Data Science Analysis Techniques
Time series forecasting analyzes sequential data points collected over time to predict future trends, relying on patterns such as seasonality and autocorrelation. Cross-sectional analysis examines data collected at a single point in time across multiple entities to identify relationships and differences among variables. These data science techniques serve distinct purposes: time series forecasting excels in temporal trend prediction, while cross-sectional analysis offers insights into static variable comparisons within a dataset.
Defining Time Series Forecasting
Time series forecasting involves analyzing sequential data points recorded over consistent time intervals to predict future values by identifying underlying patterns such as trends, seasonality, and cyclic behaviors. This approach utilizes models like ARIMA, exponential smoothing, and LSTM neural networks to capture temporal dependencies and improve accuracy. Unlike cross-sectional analysis which examines data at a single point in time, time series forecasting leverages historical temporal information to inform decision-making and strategy in domains such as finance, weather prediction, and inventory management.
Understanding Cross-Sectional Analysis
Cross-sectional analysis examines data collected at a single point in time across multiple subjects or entities, enabling comparison of variables to identify patterns and relationships. This method is essential for understanding variations and correlations within a snapshot, often used in market research, economics, and finance. Unlike time series forecasting, which predicts future trends based on historical data, cross-sectional analysis focuses on measuring and interpreting differences among units at a given moment.
Key Differences Between Time Series and Cross-Sectional Data
Time series data captures observations collected sequentially over time, enabling analysis of trends, seasonality, and temporal dependencies critical for forecasting future values. Cross-sectional data represents observations gathered at a single point in time across multiple subjects or entities, facilitating comparisons and relationships among variables without temporal ordering. Key differences include the temporal dimension inherent in time series data and the focus on simultaneous snapshot comparisons in cross-sectional analysis, impacting the choice of statistical models and forecasting approaches.
Core Algorithms Used in Time Series Forecasting
Time series forecasting primarily relies on algorithms such as ARIMA (AutoRegressive Integrated Moving Average), exponential smoothing methods like Holt-Winters, and state-space models including Kalman filters. Deep learning techniques, such as LSTM (Long Short-Term Memory) networks and Temporal Convolutional Networks (TCNs), enhance predictive accuracy by capturing complex temporal dependencies. These algorithms differ fundamentally from cross-sectional analysis methods, which focus on relationships across different entities at a single time point rather than sequential temporal data.
Essential Methods for Cross-Sectional Analysis
Cross-sectional analysis in data science primarily employs regression models, clustering algorithms, and principal component analysis to interpret relationships and patterns at a specific point in time. Techniques such as ordinary least squares (OLS) regression and logistic regression are essential for understanding dependencies among variables without temporal sequencing. Dimensionality reduction methods and unsupervised learning improve model performance by managing high-dimensional data common in cross-sectional datasets.
Applications of Time Series Forecasting in Industry
Time series forecasting is widely applied in industries such as finance for stock price prediction, retail for demand forecasting, and energy for load management. Manufacturing utilizes time series data to optimize predictive maintenance schedules, reducing downtime and costs. Healthcare leverages temporal patterns in patient data to predict outbreaks and resource needs, enhancing operational efficiency.
Cross-Sectional Analysis: Use Cases and Examples
Cross-sectional analysis in data science involves examining data collected from multiple subjects at a single point in time to identify patterns, relationships, and differences across entities. It is commonly applied in market research to compare consumer behavior across demographics, in healthcare to analyze patient outcomes among different groups, and in finance for evaluating the performance of various stocks within the same period. Examples include analyzing customer satisfaction scores across regions, comparing sales volume among product categories, and assessing income distribution within different social segments.
Evaluating Accuracy: Metrics and Validation Approaches
Time series forecasting accuracy is often evaluated using metrics such as Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE), which capture the temporal dependencies and seasonality in sequential data. Cross-sectional analysis accuracy relies on metrics like R-squared, Adjusted R-squared, and Mean Squared Error (MSE) that assess model fit across different entities at a single time point without temporal structure. Validation approaches for time series include rolling-origin evaluation and walk-forward validation to preserve temporal order, while cross-sectional analysis typically employs k-fold cross-validation to randomly partition data for unbiased model evaluation.
Choosing Between Time Series and Cross-Sectional Analysis
Choosing between time series forecasting and cross-sectional analysis depends on the dataset's structure and the research objectives. Time series forecasting analyzes sequential data points over time to predict future trends, making it ideal for financial markets, sales projections, and sensor data. Cross-sectional analysis examines data at a single point in time across multiple subjects, offering insights into relationships and patterns within variables such as demographics, customer behavior, or market segmentation.
Time Series Forecasting vs Cross-Sectional Analysis Infographic
 techiny.com
techiny.com