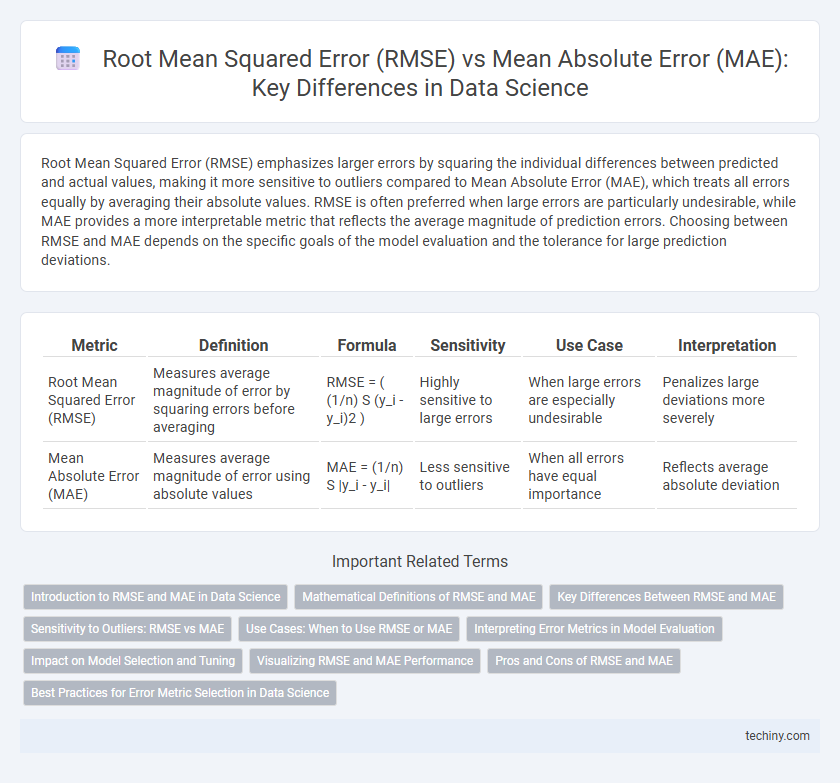
Root Mean Squared Error (RMSE) emphasizes larger errors by squaring the individual differences between predicted and actual values, making it more sensitive to outliers compared to Mean Absolute Error (MAE), which treats all errors equally by averaging their absolute values. RMSE is often preferred when large errors are particularly undesirable, while MAE provides a more interpretable metric that reflects the average magnitude of prediction errors. Choosing between RMSE and MAE depends on the specific goals of the model evaluation and the tolerance for large prediction deviations.
Table of Comparison
| Metric | Definition | Formula | Sensitivity | Use Case | Interpretation |
|---|---|---|---|---|---|
| Root Mean Squared Error (RMSE) | Measures average magnitude of error by squaring errors before averaging | RMSE = ( (1/n) S (y_i - y_i)2 ) | Highly sensitive to large errors | When large errors are especially undesirable | Penalizes large deviations more severely |
| Mean Absolute Error (MAE) | Measures average magnitude of error using absolute values | MAE = (1/n) S |y_i - y_i| | Less sensitive to outliers | When all errors have equal importance | Reflects average absolute deviation |
Introduction to RMSE and MAE in Data Science
Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) are fundamental metrics used to evaluate the accuracy of predictive models in data science. RMSE calculates the square root of the average squared differences between predicted and actual values, placing higher weight on larger errors. MAE measures the average absolute differences between predictions and true values, providing a straightforward interpretation of average error magnitude.
Mathematical Definitions of RMSE and MAE
Root Mean Squared Error (RMSE) is defined as the square root of the average of the squared differences between predicted and actual values, mathematically expressed as RMSE = sqrt((1/n) (y_i - y_i)2). Mean Absolute Error (MAE) represents the average of the absolute differences between predicted and actual values, calculated as MAE = (1/n) |y_i - y_i|. RMSE penalizes larger errors more significantly due to squaring, while MAE treats all deviations linearly, impacting how each metric reflects prediction accuracy in regression models.
Key Differences Between RMSE and MAE
Root Mean Squared Error (RMSE) penalizes larger errors more severely due to the squaring of residuals, making it sensitive to outliers, while Mean Absolute Error (MAE) treats all errors with equal weight by averaging the absolute differences between predicted and actual values. RMSE is more appropriate in contexts where large errors are particularly undesirable, as it amplifies their effect on the metric, whereas MAE provides a linear score that is more robust to outliers. The choice between RMSE and MAE depends on the specific error distribution and the importance of large deviations in the data science modeling process.
Sensitivity to Outliers: RMSE vs MAE
Root Mean Squared Error (RMSE) is highly sensitive to outliers because it squares the magnitude of errors, giving larger penalties to significant deviations. Mean Absolute Error (MAE) treats all errors linearly, resulting in a more robust measure less influenced by extreme values. In data science, RMSE is preferred when larger errors are particularly undesirable, while MAE offers a balanced metric in the presence of noisy or outlier-prone datasets.
Use Cases: When to Use RMSE or MAE
Root Mean Squared Error (RMSE) is ideal for use cases where large errors are particularly undesirable, as it penalizes them more heavily, making it suitable for applications like weather forecasting or financial risk modeling. Mean Absolute Error (MAE) is preferred in scenarios where all errors are treated equally, such as in basic regression problems or when robustness to outliers is essential. Choosing RMSE over MAE depends on the specific tolerance for error magnitude and the presence of outliers in the dataset.
Interpreting Error Metrics in Model Evaluation
Root Mean Squared Error (RMSE) amplifies larger errors, making it sensitive to outliers and useful for models where significant deviations are costly, while Mean Absolute Error (MAE) provides a straightforward average of absolute errors, offering robustness against outliers and clear interpretability. RMSE values are in the squared units of the target variable, requiring careful consideration for practical meaning, whereas MAE values share the same units as the target, facilitating direct error magnitude understanding. Selecting between RMSE and MAE depends on the error distribution and the specific consequences of large prediction errors in data science model evaluation.
Impact on Model Selection and Tuning
Root mean squared error (RMSE) emphasizes larger errors due to its squaring component, making it sensitive to outliers and often preferred when significant deviations are particularly detrimental in model selection. Mean absolute error (MAE) treats all errors equally, offering a more interpretable metric for tuning models where consistent, small errors are more critical than occasional large ones. Selecting between RMSE and MAE influences hyperparameter optimization, affecting model bias-variance trade-off and ultimately the predictive performance on unseen data.
Visualizing RMSE and MAE Performance
Visualizing RMSE and MAE performance reveals distinct error-sensitive patterns, with RMSE amplifying larger errors due to its squared component, while MAE treats all errors linearly. Graphical representations such as line plots or scatter plots highlight RMSE's pronounced peaks in datasets containing outliers, contrasting with MAE's smoother trend that reflects median model accuracy. These visual insights guide data scientists in selecting appropriate error metrics aligned with specific model evaluation goals and data distributions.
Pros and Cons of RMSE and MAE
Root Mean Squared Error (RMSE) emphasizes larger errors due to squaring residuals, making it sensitive to outliers and useful when large errors are particularly undesirable. Mean Absolute Error (MAE) provides a linear scale of error magnitude, offering robustness against outliers and easier interpretability in absolute terms. RMSE tends to penalize variance more heavily, while MAE is better suited for capturing the average model performance without disproportionately weighting extreme deviations.
Best Practices for Error Metric Selection in Data Science
Root Mean Squared Error (RMSE) is preferred when large errors need to be penalized more heavily, as it squares the residuals, emphasizing significant deviations, making it ideal for regression tasks with outliers. Mean Absolute Error (MAE) provides a linear error measure that treats all deviations equally, offering robustness against outliers and ease of interpretation in business contexts. Selecting the appropriate metric depends on the data distribution, the presence of outliers, and the specific goals of the model evaluation to ensure meaningful performance insights.
root mean squared error (RMSE) vs mean absolute error (MAE) Infographic
 techiny.com
techiny.com