PID control offers simplicity and ease of implementation for robotic motion systems by continuously adjusting control inputs based on proportional, integral, and derivative terms, making it effective for systems with predictable dynamics. LQR control provides an optimal approach by minimizing a cost function that balances state errors and control effort, resulting in improved stability and performance in complex or multi-variable robotic systems. Choosing between PID and LQR depends on the specific robotic application, system complexity, and performance requirements.
Table of Comparison
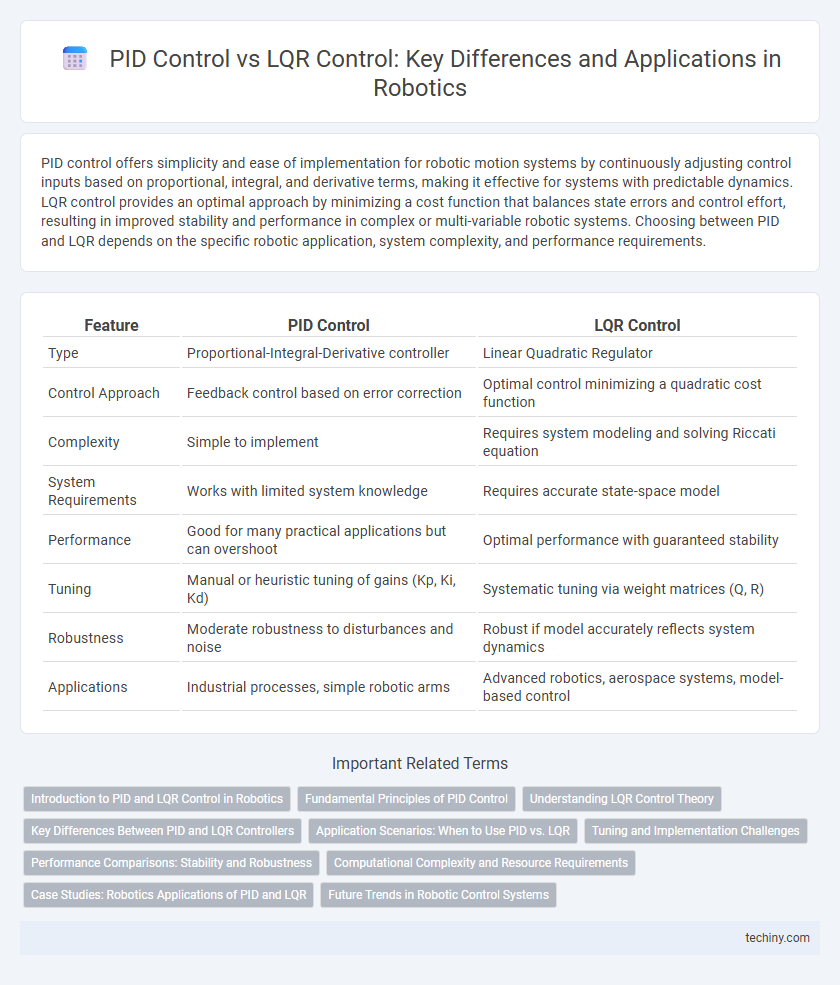
| Feature | PID Control | LQR Control |
|---|---|---|
| Type | Proportional-Integral-Derivative controller | Linear Quadratic Regulator |
| Control Approach | Feedback control based on error correction | Optimal control minimizing a quadratic cost function |
| Complexity | Simple to implement | Requires system modeling and solving Riccati equation |
| System Requirements | Works with limited system knowledge | Requires accurate state-space model |
| Performance | Good for many practical applications but can overshoot | Optimal performance with guaranteed stability |
| Tuning | Manual or heuristic tuning of gains (Kp, Ki, Kd) | Systematic tuning via weight matrices (Q, R) |
| Robustness | Moderate robustness to disturbances and noise | Robust if model accurately reflects system dynamics |
| Applications | Industrial processes, simple robotic arms | Advanced robotics, aerospace systems, model-based control |
Introduction to PID and LQR Control in Robotics
PID control in robotics relies on proportional, integral, and derivative actions to maintain desired system behavior by minimizing error signals in real-time. LQR control uses a state-space model and optimizes a cost function to achieve optimal control performance with minimal energy consumption and state deviations. Both are essential feedback control strategies, with PID favored for simplicity and LQR for handling multi-variable, complex robotic systems.
Fundamental Principles of PID Control
PID control operates on the principle of adjusting robotic system outputs by calculating the proportional, integral, and derivative of the error signal, enabling precise error correction over time. This feedback mechanism continuously compares the desired setpoint with the actual position or velocity, allowing the controller to minimize steady-state error and reduce oscillations. The simplicity and robustness of PID controllers make them effective for a wide range of robotic applications where linearity and real-time response are crucial.
Understanding LQR Control Theory
LQR control theory utilizes state-space models to minimize a quadratic cost function, providing optimal feedback gains that balance system performance and control effort. Unlike PID control, which relies on proportional, integral, and derivative terms, LQR systematically solves the Riccati equation to achieve stability and robustness in multi-variable robotic systems. This approach enhances trajectory tracking and disturbance rejection by optimizing control inputs based on the entire system state rather than just error signals.
Key Differences Between PID and LQR Controllers
PID control uses proportional, integral, and derivative gains to adjust robot actuators based on error signals, offering simplicity and ease of implementation. LQR control optimizes a quadratic cost function, balancing state error and control effort to achieve optimal feedback gains for more precise and stable system responses. While PID is suitable for systems with straightforward dynamics, LQR excels in handling multivariable, complex robotic systems with state-space models.
Application Scenarios: When to Use PID vs. LQR
PID control excels in simple, single-input single-output robotic systems requiring straightforward regulation and minimal computational resources, such as temperature or speed control. LQR control is preferred for complex, multi-input multi-output robotic systems involving state feedback and optimal performance criteria, including advanced robotic arms and autonomous vehicles. Choosing PID is effective for tasks with linear dynamics and limited disturbances, while LQR suits scenarios demanding precise stabilization and robustness under model uncertainties.
Tuning and Implementation Challenges
PID control requires manual tuning of proportional, integral, and derivative gains, which can be time-consuming and may lead to suboptimal performance in complex robotic systems. LQR control relies on solving a Riccati equation to optimize state feedback gains, offering systematic tuning but demanding an accurate model and higher computational resources. Implementing PID is simpler and more robust for non-linear or uncertain dynamics, while LQR excels in multi-variable systems with well-defined states but faces challenges in model precision and real-time computation.
Performance Comparisons: Stability and Robustness
PID control offers straightforward implementation and effective stability for a wide range of robotic systems, leveraging proportional, integral, and derivative terms to minimize error. LQR control, based on optimal control theory, provides superior robustness by minimizing a quadratic cost function, ensuring enhanced disturbance rejection and precise state regulation. Comparative studies demonstrate LQR's advantage in maintaining stability under model uncertainties and external perturbations, while PID remains preferred for simpler, less computationally intensive applications.
Computational Complexity and Resource Requirements
PID control offers lower computational complexity and minimal resource requirements, making it suitable for real-time robotic applications with limited processing power. LQR control involves solving Riccati equations, demanding higher computational capability and memory, often requiring specialized hardware for high-dimensional systems. The trade-off between simplicity in PID and optimality in LQR depends on the robot's hardware constraints and control performance needs.
Case Studies: Robotics Applications of PID and LQR
PID control excels in robotic arm manipulation tasks due to its simplicity and real-time responsiveness, particularly in systems with steady-state errors and noise disturbances. LQR control demonstrates superior performance in mobile robot trajectory tracking, optimizing energy efficiency and stability through state feedback and system dynamics modeling. Comparative case studies reveal that while PID suits straightforward control loops, LQR offers enhanced precision and robustness in complex, multivariable robotic systems.
Future Trends in Robotic Control Systems
Future trends in robotic control systems emphasize the integration of advanced machine learning algorithms with traditional PID and LQR control methods to enhance adaptability and precision. Model Predictive Control (MPC) and adaptive LQR are gaining prominence for handling nonlinear dynamics and uncertainties in real-time robotic applications. The fusion of data-driven optimization with classical control theory paves the way for highly efficient, robust, and autonomous robotic platforms.
PID Control vs LQR Control Infographic
 techiny.com
techiny.com