Perplexity measures how well a probability model predicts a sample and is derived from the exponentiation of cross-entropy, reflecting the model's uncertainty in predicting a sequence. Cross-entropy quantifies the difference between the true distribution and the predicted probabilities, serving as a loss function during the training of AI language models. Lower cross-entropy corresponds to reduced perplexity, indicating improved model performance in generating accurate predictions.
Table of Comparison
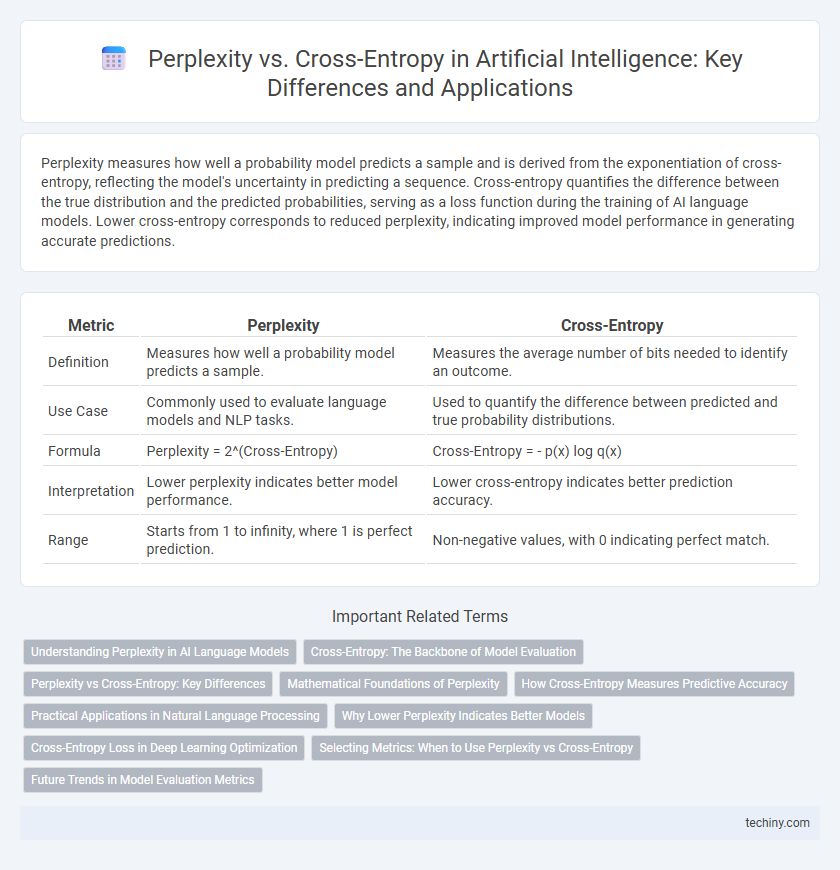
| Metric | Perplexity | Cross-Entropy |
|---|---|---|
| Definition | Measures how well a probability model predicts a sample. | Measures the average number of bits needed to identify an outcome. |
| Use Case | Commonly used to evaluate language models and NLP tasks. | Used to quantify the difference between predicted and true probability distributions. |
| Formula | Perplexity = 2^(Cross-Entropy) | Cross-Entropy = - p(x) log q(x) |
| Interpretation | Lower perplexity indicates better model performance. | Lower cross-entropy indicates better prediction accuracy. |
| Range | Starts from 1 to infinity, where 1 is perfect prediction. | Non-negative values, with 0 indicating perfect match. |
Understanding Perplexity in AI Language Models
Perplexity measures how well an AI language model predicts a sample by calculating the exponential of the average negative log-likelihood, reflecting the model's uncertainty in predicting the next word. Lower perplexity indicates a more accurate and confident model, aligning closely with better performance in natural language understanding tasks. Cross-entropy loss, directly related to perplexity, quantifies the difference between the predicted probability distribution and the true distribution, serving as the fundamental training objective for models like GPT and BERT.
Cross-Entropy: The Backbone of Model Evaluation
Cross-entropy measures the divergence between predicted probabilities and actual outcomes, serving as a fundamental loss function in training AI models. It quantifies the inefficiency of predictions, making it essential for optimizing neural networks in tasks like classification and language modeling. High cross-entropy values indicate poor model performance, guiding improvements in parameters to enhance accuracy and reliability.
Perplexity vs Cross-Entropy: Key Differences
Perplexity and cross-entropy both measure the performance of language models by evaluating prediction accuracy, with perplexity representing the exponential of the cross-entropy loss, thereby indicating how well a model predicts a sample. Cross-entropy quantifies the difference between the predicted probability distribution and the true distribution, providing a direct measure of uncertainty, while perplexity translates this uncertainty into an interpretable scale reflecting the model's average branching factor when making predictions. Understanding the relationship between these metrics is essential for optimizing language models in artificial intelligence applications.
Mathematical Foundations of Perplexity
Perplexity mathematically quantifies the uncertainty of a language model by exponentiating the cross-entropy loss, reflecting the average branching factor in predicting word sequences. Defined as 2 raised to the power of the cross-entropy, perplexity measures the weighted geometric mean of the predicted probabilities, capturing how well the model predicts a sample. Lower perplexity values indicate more confident and accurate predictions, directly linking to cross-entropy's role as the expectation of the negative log-likelihood over true data distributions.
How Cross-Entropy Measures Predictive Accuracy
Cross-entropy quantifies predictive accuracy by measuring the difference between the predicted probability distribution and the actual label distribution in classification tasks. It calculates the average number of bits needed to encode the true labels given the model's predicted probabilities, effectively penalizing confident but incorrect predictions. Lower cross-entropy values indicate higher predictive accuracy as the predicted probabilities closely match the true outcomes.
Practical Applications in Natural Language Processing
Perplexity measures how well a probabilistic model predicts a sample by evaluating the exponentiation of the cross-entropy loss, directly correlating with the model's uncertainty in language generation tasks. In natural language processing, optimizing perplexity leads to improved language models for tasks such as text prediction, machine translation, and speech recognition. Cross-entropy loss functions serve as the foundation for training these models by quantifying the divergence between predicted and actual word distributions, ultimately enhancing model accuracy and fluency.
Why Lower Perplexity Indicates Better Models
Lower perplexity in artificial intelligence language models signifies better performance because it reflects the model's improved ability to predict a sequence of words accurately. Perplexity measures the exponentiated average negative log-likelihood, so lower values correspond to higher probability assignments to the actual next words in a sentence. This efficiency in prediction directly correlates with reduced cross-entropy loss, indicating precise language understanding and generation.
Cross-Entropy Loss in Deep Learning Optimization
Cross-entropy loss is a critical metric in deep learning optimization, quantifying the difference between predicted probabilities and actual labels by measuring the dissimilarity between two probability distributions. It effectively penalizes incorrect predictions, guiding neural networks to minimize uncertainty and improve accuracy during training. Compared to perplexity, which represents the exponentiated cross-entropy and reflects the model's uncertainty, cross-entropy loss provides a more straightforward gradient for optimization algorithms to converge efficiently.
Selecting Metrics: When to Use Perplexity vs Cross-Entropy
Perplexity measures how well a probabilistic model predicts a sample by quantifying uncertainty, ideal for evaluating language models in natural language processing tasks where interpretability in terms of branching choices is crucial. Cross-entropy directly calculates the difference between the predicted probability distribution and the true distribution, offering a more granular loss measurement suitable for training deep learning models with backpropagation. Selecting between perplexity and cross-entropy depends on whether interpretability of model uncertainty (perplexity) or precise optimization of prediction error (cross-entropy) is the priority in AI model evaluation and tuning.
Future Trends in Model Evaluation Metrics
Future trends in model evaluation metrics emphasize evolving beyond traditional perplexity and cross-entropy by integrating more nuanced measures that capture model interpretability and contextual understanding. Techniques leveraging contrastive learning and embedding-based metrics are gaining prominence for evaluating the semantic coherence of AI outputs. These advancements aim to refine performance benchmarks, enabling AI systems to demonstrate greater reliability in complex, real-world language tasks.
Perplexity vs cross-entropy Infographic
 techiny.com
techiny.com