Greedy algorithms make decisions based on the best immediate option, aiming for a quick, locally optimal solution that may not yield the overall best result. Dynamic programming solves problems by breaking them into overlapping subproblems, storing intermediate results to ensure an optimal global solution efficiently. Understanding when to use greedy algorithms versus dynamic programming is crucial for optimizing artificial intelligence tasks such as pathfinding, resource allocation, and sequence analysis.
Table of Comparison
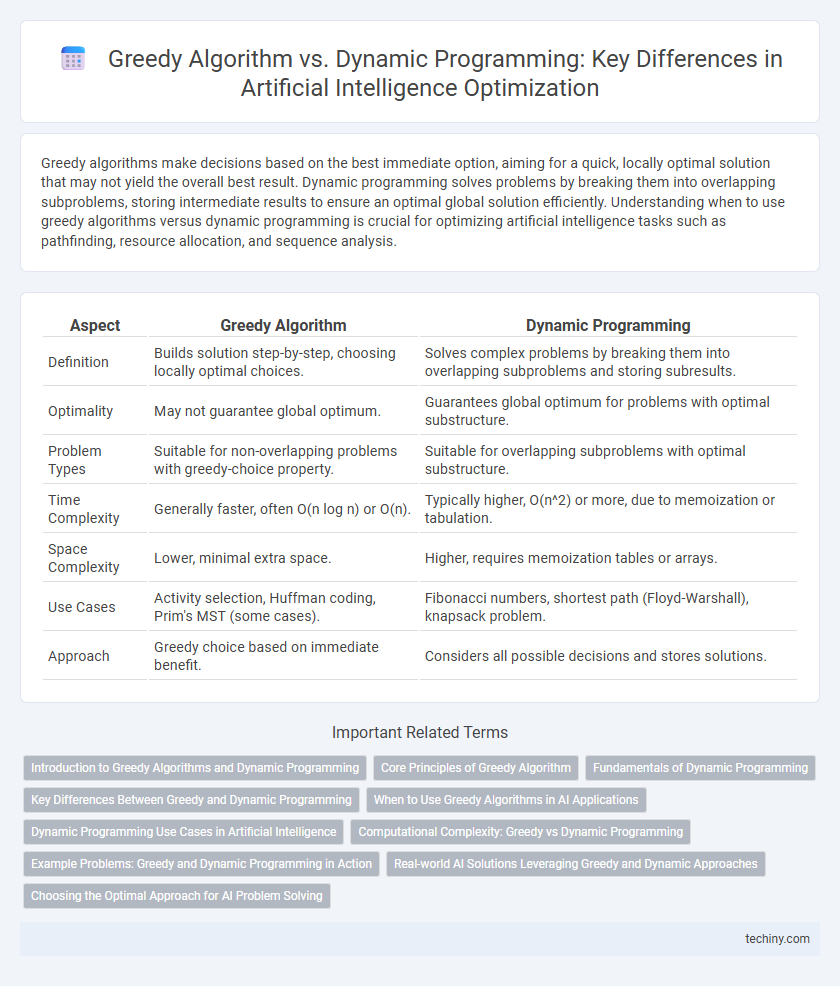
| Aspect | Greedy Algorithm | Dynamic Programming |
|---|---|---|
| Definition | Builds solution step-by-step, choosing locally optimal choices. | Solves complex problems by breaking them into overlapping subproblems and storing subresults. |
| Optimality | May not guarantee global optimum. | Guarantees global optimum for problems with optimal substructure. |
| Problem Types | Suitable for non-overlapping problems with greedy-choice property. | Suitable for overlapping subproblems with optimal substructure. |
| Time Complexity | Generally faster, often O(n log n) or O(n). | Typically higher, O(n^2) or more, due to memoization or tabulation. |
| Space Complexity | Lower, minimal extra space. | Higher, requires memoization tables or arrays. |
| Use Cases | Activity selection, Huffman coding, Prim's MST (some cases). | Fibonacci numbers, shortest path (Floyd-Warshall), knapsack problem. |
| Approach | Greedy choice based on immediate benefit. | Considers all possible decisions and stores solutions. |
Introduction to Greedy Algorithms and Dynamic Programming
Greedy algorithms build solutions by making the locally optimal choice at each step, aiming for a global optimum without revisiting previous decisions, which can be efficient but may not always yield the best solution. Dynamic programming solves complex problems by breaking them down into overlapping subproblems, storing intermediate results to avoid redundant computations and ensuring an optimal solution. Both techniques address optimization tasks but differ in approach and applicability, with dynamic programming suited for problems exhibiting optimal substructure and overlapping subproblems, while greedy algorithms apply when the problem possesses the greedy-choice property.
Core Principles of Greedy Algorithm
The core principles of the Greedy Algorithm involve making a sequence of choices, each of which looks best at the moment, to find a globally optimal solution. It relies on the properties of optimal substructure and the greedy-choice property, where local optimization leads to global optimization without revisiting previous decisions. This approach is efficient for problems like minimum spanning trees and shortest paths, but it may not work for all optimization problems, especially those requiring reconsideration of earlier choices.
Fundamentals of Dynamic Programming
Dynamic Programming (DP) solves complex problems by breaking them down into simpler overlapping subproblems and storing their solutions to avoid redundant computations, optimizing time efficiency. Unlike Greedy Algorithms, which make locally optimal choices at each step, DP ensures global optimality by systematically exploring all solution possibilities through memoization or tabulation. Core principles of DP include optimal substructure, overlapping subproblems, and the use of recursion combined with caching to improve computational performance in artificial intelligence applications.
Key Differences Between Greedy and Dynamic Programming
Greedy algorithms make locally optimal choices at each step with the hope of finding a global optimum, while dynamic programming solves problems by breaking them down into overlapping subproblems and storing their solutions to avoid redundant computations. Greedy algorithms typically have faster execution times and simpler implementations but may fail on problems that require exploring multiple solutions, whereas dynamic programming guarantees optimal solutions for problems exhibiting optimal substructure and overlapping subproblems. Key differences involve problem applicability, solution optimality, and computational complexity, with dynamic programming being more suitable for complex optimization tasks in artificial intelligence.
When to Use Greedy Algorithms in AI Applications
Greedy algorithms are ideal in AI applications when the problem exhibits the greedy-choice property and optimal substructure, allowing decisions to be made locally at each step for a globally optimal solution. They excel in scenarios such as shortest path finding, minimum spanning trees, and scheduling problems where computational efficiency is critical. Choosing greedy algorithms prioritizes speed and simplicity over exhaustive search, making them suitable for real-time AI systems or large-scale optimization tasks.
Dynamic Programming Use Cases in Artificial Intelligence
Dynamic programming is widely used in artificial intelligence for optimizing decision-making processes in complex problems with overlapping subproblems and optimal substructure, such as in reinforcement learning for policy evaluation and in natural language processing for parsing algorithms. It enables efficient computation of solutions by storing intermediate results, significantly reducing time complexity compared to naive recursive approaches. Key applications include sequence alignment in bioinformatics, resource allocation, and predictive modeling in machine learning tasks.
Computational Complexity: Greedy vs Dynamic Programming
Greedy algorithms typically operate with lower computational complexity, often achieving linear or polynomial time due to their straightforward, stepwise optimization approach. Dynamic programming, while generally more computationally intensive with polynomial time complexity like O(n^2) or O(n^3), systematically solves overlapping subproblems to guarantee optimal solutions. The trade-off between the two lies in greedy algorithms offering faster execution but potentially suboptimal results, whereas dynamic programming ensures optimality at the cost of higher computational resources.
Example Problems: Greedy and Dynamic Programming in Action
Greedy algorithms excel in problems like the Activity Selection Problem, where selecting the local optimum leads to a global solution efficiently by choosing the earliest finishing activity. In contrast, dynamic programming tackles complex cases such as the Knapsack Problem by breaking it down into overlapping subproblems and storing intermediate results to optimize overall value. Both approaches highlight different strategies: greedy prioritizes immediate gains, while dynamic programming emphasizes comprehensive optimization through memorization.
Real-world AI Solutions Leveraging Greedy and Dynamic Approaches
Real-world AI solutions often balance Greedy Algorithms' efficiency with Dynamic Programming's thoroughness to optimize decision-making processes. Greedy Algorithms excel in scenarios requiring fast, approximate solutions such as routing in autonomous vehicles, while Dynamic Programming provides exact results for complex problems like natural language processing and reinforcement learning. Leveraging these complementary approaches enhances AI's ability to handle diverse optimization challenges in fields including robotics, finance, and healthcare.
Choosing the Optimal Approach for AI Problem Solving
Greedy algorithms are suitable for AI problem-solving when the problem exhibits the greedy-choice property and optimal substructure, allowing local optimal choices to lead to a globally optimal solution efficiently. Dynamic programming excels in AI scenarios involving overlapping subproblems and complex dependencies, where it systematically stores intermediate results to avoid redundant computations and ensures finding the global optimum. Selecting the optimal approach depends on problem characteristics such as input size, optimal substructure presence, and whether subproblems overlap, guiding AI practitioners to balance computational efficiency and solution accuracy.
Greedy Algorithm vs Dynamic Programming Infographic
 techiny.com
techiny.com