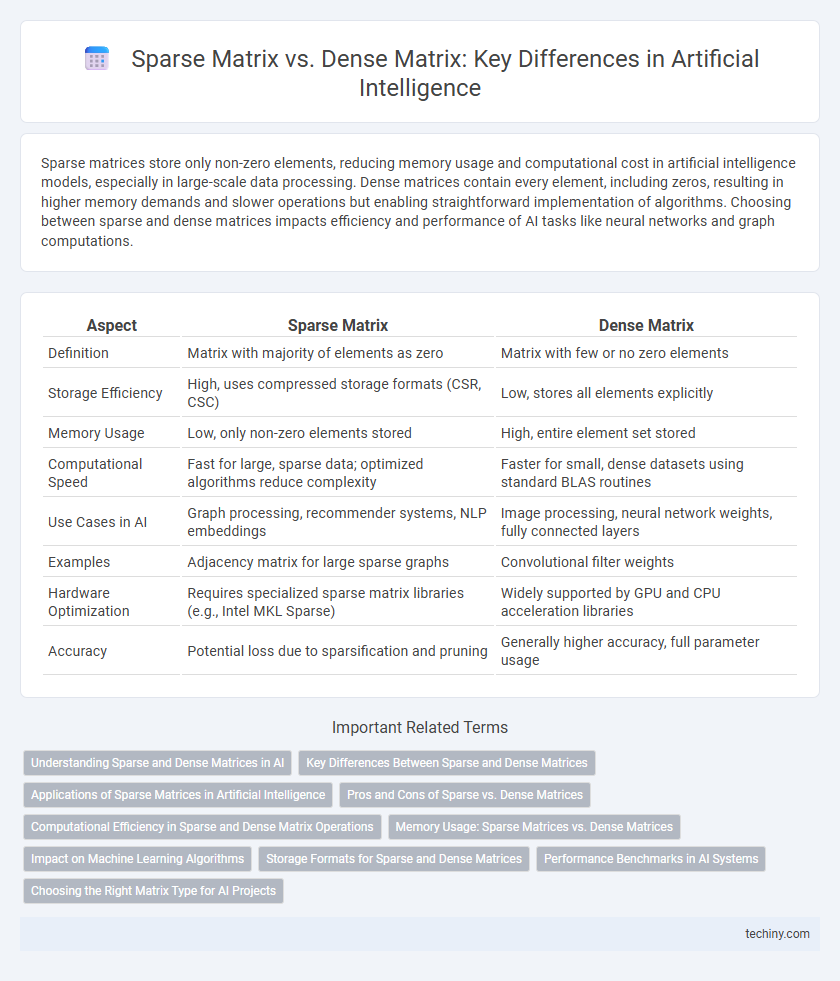
Sparse matrices store only non-zero elements, reducing memory usage and computational cost in artificial intelligence models, especially in large-scale data processing. Dense matrices contain every element, including zeros, resulting in higher memory demands and slower operations but enabling straightforward implementation of algorithms. Choosing between sparse and dense matrices impacts efficiency and performance of AI tasks like neural networks and graph computations.
Table of Comparison
| Aspect | Sparse Matrix | Dense Matrix |
|---|---|---|
| Definition | Matrix with majority of elements as zero | Matrix with few or no zero elements |
| Storage Efficiency | High, uses compressed storage formats (CSR, CSC) | Low, stores all elements explicitly |
| Memory Usage | Low, only non-zero elements stored | High, entire element set stored |
| Computational Speed | Fast for large, sparse data; optimized algorithms reduce complexity | Faster for small, dense datasets using standard BLAS routines |
| Use Cases in AI | Graph processing, recommender systems, NLP embeddings | Image processing, neural network weights, fully connected layers |
| Examples | Adjacency matrix for large sparse graphs | Convolutional filter weights |
| Hardware Optimization | Requires specialized sparse matrix libraries (e.g., Intel MKL Sparse) | Widely supported by GPU and CPU acceleration libraries |
| Accuracy | Potential loss due to sparsification and pruning | Generally higher accuracy, full parameter usage |
Understanding Sparse and Dense Matrices in AI
Sparse matrices in AI contain predominantly zero elements, optimizing memory usage and computational efficiency for large-scale data such as graph representations and natural language processing. Dense matrices, filled with mostly non-zero elements, are suitable for applications requiring complete data representation, like image processing and neural network weight calculations. Understanding the differences in storage methods and computational impact aids in selecting appropriate matrix types for AI model performance and scalability.
Key Differences Between Sparse and Dense Matrices
Sparse matrices store predominantly zero elements efficiently by only recording non-zero values and their indices, drastically reducing memory usage compared to dense matrices, which allocate space for all elements regardless of value. Sparse matrix operations leverage specialized algorithms optimized for non-zero elements, leading to faster computation in large-scale AI models where data sparsity is common, unlike dense matrices which process every element uniformly. Key differences include memory footprint, computational efficiency, and applicability to AI tasks such as natural language processing and graph neural networks where sparse representations are predominant.
Applications of Sparse Matrices in Artificial Intelligence
Sparse matrices play a crucial role in artificial intelligence applications such as natural language processing, recommendation systems, and graph-based learning, where data is inherently high-dimensional but contains numerous zero elements. Their efficient storage and computation enable faster processing and reduced memory usage compared to dense matrices, particularly in large-scale machine learning models and neural networks. Exploiting sparsity improves scalability and performance in algorithms like collaborative filtering, topic modeling, and deep learning with sparse input features.
Pros and Cons of Sparse vs. Dense Matrices
Sparse matrices significantly reduce memory usage and computational complexity by storing only non-zero elements, making them ideal for large-scale AI models with predominantly zero values. Dense matrices provide straightforward access and efficient computation for smaller datasets or models with few zero entries but incur higher storage costs and can slow down processing when many zeros are present. Choosing between sparse and dense matrices depends on dataset sparsity, computational resources, and specific AI algorithm requirements.
Computational Efficiency in Sparse and Dense Matrix Operations
Sparse matrix operations are computationally more efficient than dense matrix operations when dealing with large datasets containing many zero elements, as they leverage storage formats that avoid processing irrelevant zeros, reducing memory usage and computation time. Dense matrix operations require extensive computational resources because every element is processed, leading to inefficiencies in cases where matrices have predominantly zero values. Optimizing algorithms for sparse matrices, such as compressed sparse row (CSR) or compressed sparse column (CSC) formats, significantly accelerates matrix-vector multiplication and other linear algebra tasks critical in AI applications like neural networks and graph processing.
Memory Usage: Sparse Matrices vs. Dense Matrices
Sparse matrices significantly reduce memory usage by storing only non-zero elements and their indices, unlike dense matrices which allocate memory for every element regardless of value. This efficiency becomes critical in AI applications involving large-scale data, such as natural language processing and graph algorithms, where sparsity is common. Reducing memory overhead enables faster computations and scalability in machine learning models.
Impact on Machine Learning Algorithms
Sparse matrices, characterized by a high proportion of zero elements, reduce memory usage and computational complexity in machine learning algorithms, particularly in large-scale data scenarios such as natural language processing and recommender systems. Dense matrices, containing mostly non-zero elements, often require more storage and computational resources but enable more straightforward mathematical operations, benefiting algorithms reliant on continuous data like neural networks. The choice between sparse and dense matrix representations significantly influences algorithm performance, scalability, and resource efficiency in AI model training and inference tasks.
Storage Formats for Sparse and Dense Matrices
Sparse matrices are efficiently stored using compressed storage formats such as Compressed Sparse Row (CSR) and Compressed Sparse Column (CSC), which store only non-zero elements and their indices, significantly reducing memory usage. Dense matrices utilize straightforward storage schemes like row-major or column-major order, storing every element explicitly, which can lead to higher memory consumption for large datasets. Choosing the appropriate storage format impacts computational performance in AI applications, as sparse formats minimize redundancy and dense formats facilitate faster arithmetic operations on fully populated data.
Performance Benchmarks in AI Systems
Sparse matrices significantly reduce memory usage and computational overhead by storing only non-zero elements, leading to faster training and inference in AI systems with high-dimensional data. In contrast, dense matrices consume more memory and processing power, often resulting in slower performance for large, sparse datasets commonly found in natural language processing and recommendation systems. Benchmark studies reveal that AI models leveraging sparse matrix operations achieve up to 10x speedup and improved scalability compared to dense matrix counterparts, especially on GPU-accelerated hardware.
Choosing the Right Matrix Type for AI Projects
Sparse matrices optimize memory use by storing only non-zero elements, making them ideal for large-scale AI projects involving high-dimensional data with many zero values, such as natural language processing and recommendation systems. Dense matrices store all elements explicitly, providing faster computation suited for smaller datasets or AI models requiring full matrix operations like deep learning layers. Selecting the right matrix type depends on data sparsity, computational resources, and specific algorithm requirements to ensure efficient processing and model performance.
Sparse Matrix vs Dense Matrix Infographic
 techiny.com
techiny.com