Autoencoders and principal component analysis (PCA) both perform dimensionality reduction, but autoencoders leverage nonlinear transformations through neural networks, enabling them to capture complex data patterns beyond PCA's linear approach. PCA identifies orthogonal axes of maximum variance to reduce data dimensions efficiently, while autoencoders learn compact data representations by minimizing reconstruction error through encoding and decoding layers. The flexibility of autoencoders often leads to superior performance in handling high-dimensional and nonlinear datasets compared to PCA's straightforward linear mappings.
Table of Comparison
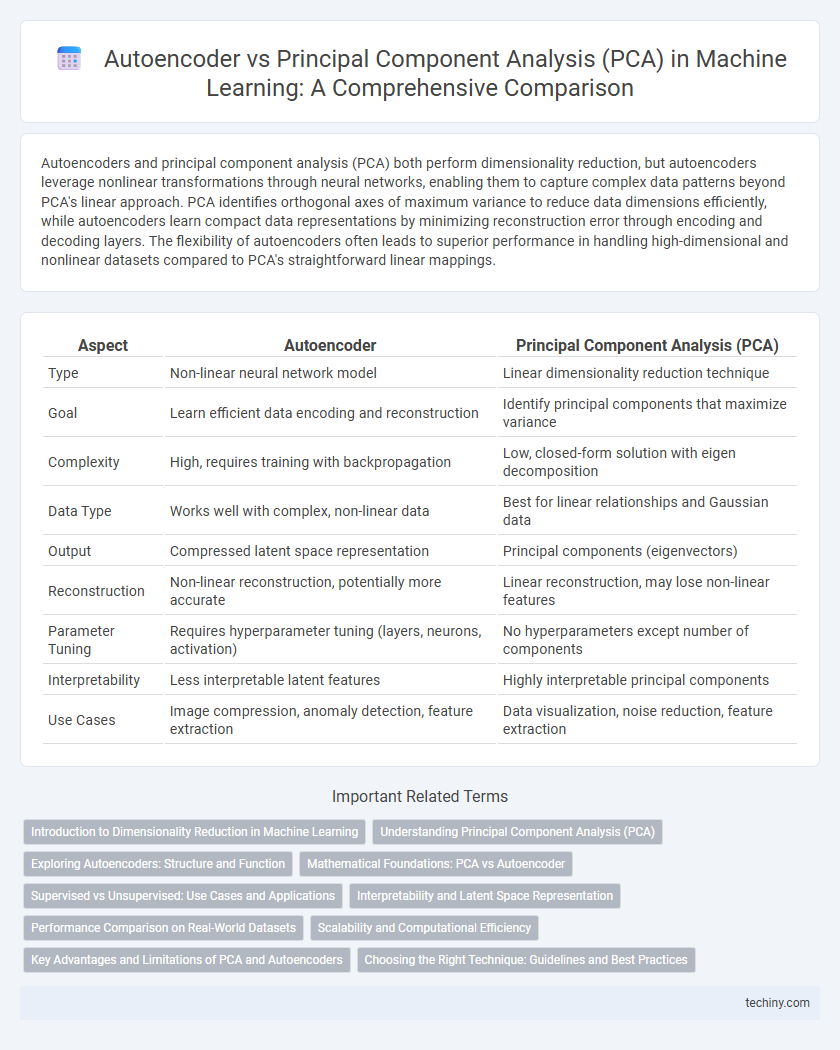
| Aspect | Autoencoder | Principal Component Analysis (PCA) |
|---|---|---|
| Type | Non-linear neural network model | Linear dimensionality reduction technique |
| Goal | Learn efficient data encoding and reconstruction | Identify principal components that maximize variance |
| Complexity | High, requires training with backpropagation | Low, closed-form solution with eigen decomposition |
| Data Type | Works well with complex, non-linear data | Best for linear relationships and Gaussian data |
| Output | Compressed latent space representation | Principal components (eigenvectors) |
| Reconstruction | Non-linear reconstruction, potentially more accurate | Linear reconstruction, may lose non-linear features |
| Parameter Tuning | Requires hyperparameter tuning (layers, neurons, activation) | No hyperparameters except number of components |
| Interpretability | Less interpretable latent features | Highly interpretable principal components |
| Use Cases | Image compression, anomaly detection, feature extraction | Data visualization, noise reduction, feature extraction |
Introduction to Dimensionality Reduction in Machine Learning
Autoencoders and Principal Component Analysis (PCA) are fundamental techniques for dimensionality reduction in machine learning, aiming to simplify data representation while preserving essential features. PCA achieves this by projecting data onto lower-dimensional linear subspaces based on variance maximization, whereas autoencoders utilize neural networks to learn nonlinear encoding and decoding functions that capture complex data structures. Both methods enhance model performance and reduce computational cost by mitigating the curse of dimensionality and improving feature extraction.
Understanding Principal Component Analysis (PCA)
Principal Component Analysis (PCA) is a linear dimensionality reduction technique that transforms high-dimensional data into a lower-dimensional form by identifying the directions (principal components) of maximum variance. It uses eigenvalue decomposition of the covariance matrix to capture the most significant features, preserving essential information while reducing noise and redundancy. PCA is widely used for feature extraction, data visualization, and preprocessing in machine learning tasks, especially when interpretability and computational efficiency are critical.
Exploring Autoencoders: Structure and Function
Autoencoders are neural networks designed to learn efficient data representations through a bottleneck architecture, compressing input data into lower-dimensional latent space and reconstructing it with minimal loss. Unlike Principal Component Analysis (PCA), which relies on linear transformations to reduce dimensionality, autoencoders capture complex, nonlinear relationships within the data by leveraging multilayered encoder-decoder structures. This ability to model intricate features makes autoencoders highly effective for tasks such as anomaly detection, image denoising, and feature extraction in machine learning.
Mathematical Foundations: PCA vs Autoencoder
Principal Component Analysis (PCA) relies on linear algebra, specifically eigen decomposition of the covariance matrix, to identify orthogonal directions of maximum variance, producing a linear dimensionality reduction. Autoencoders utilize nonlinear neural network architectures that learn a compressed representation by minimizing reconstruction error through backpropagation, allowing them to capture complex, nonlinear data structures. The mathematical foundation of PCA is rooted in linear transform theory, while autoencoders are based on optimization techniques in deep learning, enabling richer feature extraction beyond linear subspaces.
Supervised vs Unsupervised: Use Cases and Applications
Autoencoders excel in unsupervised learning tasks for complex data compression and feature extraction, effectively capturing nonlinear relationships in images and audio datasets. Principal Component Analysis (PCA), a linear dimensionality reduction technique, is widely used in exploratory data analysis and preprocessing, especially for supervised learning pipelines requiring noise reduction and feature decorrelation. Both methods are critical in feature engineering but differ in adaptability: autoencoders can be fine-tuned for supervised tasks like anomaly detection, while PCA primarily serves as an unsupervised step before supervised modeling.
Interpretability and Latent Space Representation
Autoencoders create nonlinear latent space representations that capture complex data structures, making them less interpretable but more flexible than Principal Component Analysis (PCA), which provides linear, orthogonal components that are easier to interpret. PCA's latent space corresponds to directions of maximum variance, facilitating straightforward understanding of feature contributions, whereas autoencoders' latent variables are typically abstract and require additional analysis for interpretability. The trade-off involves PCA offering clear principal components for dimensionality reduction, while autoencoders enable richer feature encoding at the cost of reduced transparency.
Performance Comparison on Real-World Datasets
Autoencoders demonstrate superior performance over Principal Component Analysis (PCA) on complex real-world datasets by capturing non-linear relationships through deep neural network architectures, resulting in more accurate data reconstruction and feature extraction. PCA, while computationally efficient and effective for linear dimensionality reduction, often underperforms when dealing with intricate structures or high-dimensional data where non-linearity is significant. Empirical studies reveal that autoencoders achieve lower reconstruction error and better generalization on datasets such as image recognition, speech processing, and genomics, validating their advantage in practical machine learning applications.
Scalability and Computational Efficiency
Autoencoders offer greater scalability compared to Principal Component Analysis (PCA) as they can handle large, high-dimensional datasets and complex nonlinear relationships through deep neural network architectures. PCA is computationally efficient for smaller or moderate-sized datasets since it relies on linear algebra operations like eigen decomposition but becomes less practical as dataset size and dimensionality increase. Autoencoders leverage GPU acceleration and batch processing to improve training speed, making them more suitable for big data applications in machine learning.
Key Advantages and Limitations of PCA and Autoencoders
Principal Component Analysis (PCA) excels at linear dimensionality reduction and offers interpretability with low computational cost, but it struggles with capturing nonlinear relationships in data. Autoencoders, leveraging neural networks, can model complex nonlinear patterns and achieve more flexible feature extraction, though they require larger datasets and careful tuning to avoid overfitting. PCA provides an efficient, unsupervised technique ideal for simple data structures, whereas autoencoders offer powerful, adaptable representations at the expense of higher complexity and training time.
Choosing the Right Technique: Guidelines and Best Practices
When selecting between autoencoders and principal component analysis (PCA) for dimensionality reduction in machine learning, consider the complexity of the data and the need for non-linear feature extraction. Autoencoders excel with large, high-dimensional datasets and can capture complex patterns through deep neural networks, while PCA is effective for linear correlations and offers faster computation with interpretability. Best practices involve evaluating reconstruction error, computational resources, and the specific task requirements to determine the most suitable technique.
autoencoder vs principal component analysis Infographic
 techiny.com
techiny.com