Cross-entropy loss is widely used for probabilistic classification tasks due to its ability to measure the difference between predicted probability distributions and true labels, optimizing models for better probability calibration. Hinge loss, commonly associated with support vector machines, focuses on maximizing the margin between classes, promoting robust decision boundaries by penalizing predictions not confidently on the correct side. Selecting between cross-entropy and hinge loss depends on the problem specifics, with cross-entropy favoring likelihood optimization and hinge loss emphasizing margin maximization.
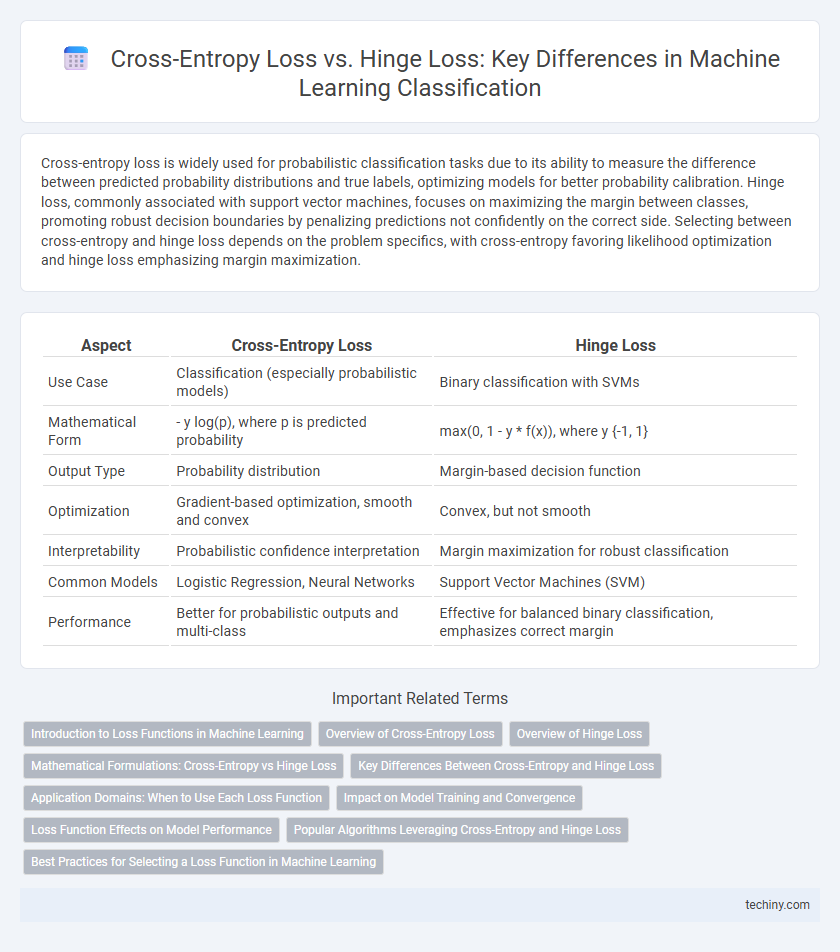
Table of Comparison
| Aspect | Cross-Entropy Loss | Hinge Loss |
|---|---|---|
| Use Case | Classification (especially probabilistic models) | Binary classification with SVMs |
| Mathematical Form | - y log(p), where p is predicted probability | max(0, 1 - y * f(x)), where y {-1, 1} |
| Output Type | Probability distribution | Margin-based decision function |
| Optimization | Gradient-based optimization, smooth and convex | Convex, but not smooth |
| Interpretability | Probabilistic confidence interpretation | Margin maximization for robust classification |
| Common Models | Logistic Regression, Neural Networks | Support Vector Machines (SVM) |
| Performance | Better for probabilistic outputs and multi-class | Effective for balanced binary classification, emphasizes correct margin |
Introduction to Loss Functions in Machine Learning
Cross-entropy loss measures the difference between predicted probabilities and actual class labels, making it ideal for classification tasks with probabilistic outputs. Hinge loss is primarily used with Support Vector Machines, focusing on maximizing the margin between classes to improve classification robustness. Both loss functions guide the optimization process but differ in their approach to penalizing misclassifications and margin violations.
Overview of Cross-Entropy Loss
Cross-entropy loss measures the difference between two probability distributions, typically the predicted probability distribution and the true distribution, making it ideal for classification tasks. It quantifies the performance of a classification model by penalizing incorrect predictions more heavily when the predicted probability diverges significantly from the actual label. Commonly used in logistic regression and neural networks, cross-entropy loss enhances model accuracy by optimizing probability outputs directly.
Overview of Hinge Loss
Hinge loss is a popular loss function used primarily for training support vector machines (SVMs) and maximum-margin classifiers. It measures the distance between the predicted margin and the true label, penalizing predictions that fall within or on the wrong side of the margin boundary, encouraging a decision boundary with maximum margin. Unlike cross-entropy loss, hinge loss is not probabilistic and is particularly effective for binary classification problems where margin maximization is critical.
Mathematical Formulations: Cross-Entropy vs Hinge Loss
Cross-entropy loss is mathematically defined as -y_i log(p_i), where y_i represents the true class label and p_i is the predicted probability for class i, optimizing probabilistic outputs in classification tasks. Hinge loss, formulated as max(0, 1 - y_i f(x_i)), where y_i is the true label and f(x_i) the prediction score, emphasizes margin maximization particularly in support vector machines. Cross-entropy focuses on probability distribution alignment while hinge loss prioritizes margin-based separation between classes.
Key Differences Between Cross-Entropy and Hinge Loss
Cross-entropy loss measures the performance of classification models by comparing the predicted probabilities to the actual class labels, optimizing for probabilistic outputs, while hinge loss is primarily used for maximum-margin classification in support vector machines, focusing on the margin between classes. Cross-entropy applies a logarithmic penalty that heavily penalizes incorrect confident predictions, whereas hinge loss imposes a linear penalty when the margin is violated, promoting larger separations between decision boundaries. The choice between these losses impacts model interpretability, convergence behavior, and suitability for probabilistic outputs versus margin-based classifiers.
Application Domains: When to Use Each Loss Function
Cross-entropy loss is widely used in classification tasks involving probabilistic outputs, such as image recognition, natural language processing, and multi-class problems, due to its ability to measure the distance between predicted probabilities and true labels effectively. Hinge loss is primarily applied in binary classification scenarios with support vector machines, emphasizing margin maximization for clear decision boundaries and often preferred in text classification and some structured prediction tasks. Selecting cross-entropy loss benefits neural networks handling probabilistic interpretations, while hinge loss suits models prioritizing margin-based optimization and robustness to misclassified samples.
Impact on Model Training and Convergence
Cross-entropy loss, commonly used in classification tasks, promotes probabilistic interpretations by penalizing incorrect predictions with a gradient that smoothly guides model weights, resulting in faster and more stable convergence. Hinge loss, primarily in support vector machines, enforces a margin between classes, enhancing model robustness but often leading to slower convergence due to its piecewise linear nature. The choice between cross-entropy and hinge loss significantly influences training dynamics, with cross-entropy favoring quicker optimization and hinge loss encouraging stronger class separation in the learned representations.
Loss Function Effects on Model Performance
Cross-entropy loss enhances probabilistic interpretations by penalizing incorrect classifications proportionally to their confidence, leading to smoother gradient updates and faster convergence in neural networks. Hinge loss enforces a margin between classes, promoting robust decision boundaries beneficial for support vector machines and improving generalization on linearly separable data. Selecting the appropriate loss function critically impacts model performance by influencing gradient behavior, convergence speed, and the ability to handle class overlap or imbalance.
Popular Algorithms Leveraging Cross-Entropy and Hinge Loss
Cross-entropy loss is widely leveraged in popular algorithms such as logistic regression, neural networks, and deep learning models for classification tasks due to its probabilistic interpretation and smooth gradient properties. Hinge loss is prominently used in support vector machines (SVMs) and structured output learning to maximize the margin between classes, enhancing model generalization on classification problems. Both loss functions serve distinct roles: cross-entropy optimizes probabilistic predictions, while hinge loss focuses on margin maximization for robust decision boundaries.
Best Practices for Selecting a Loss Function in Machine Learning
Selecting the appropriate loss function depends on the specific machine learning task and model architecture; cross-entropy loss is typically preferred for probabilistic classification problems due to its smooth gradient and probabilistic interpretation. Hinge loss is often favored in support vector machines for margin maximization in binary classification, promoting robustness against misclassifications. Evaluating the dataset's characteristics, model complexity, and convergence behavior guides the best practice decision between cross-entropy and hinge loss to optimize performance.
cross-entropy loss vs hinge loss Infographic
 techiny.com
techiny.com