Cross-validation divides the dataset into multiple folds to assess model performance by training and testing on different subsets, ensuring robust evaluation with reduced overfitting risk. Bootstrapping generates multiple resampled datasets with replacement, enabling estimation of model accuracy and variance without the need for explicit data splitting. While cross-validation emphasizes systematic data partitioning, bootstrapping relies on random sampling to provide confidence intervals for predictive metrics.
Table of Comparison
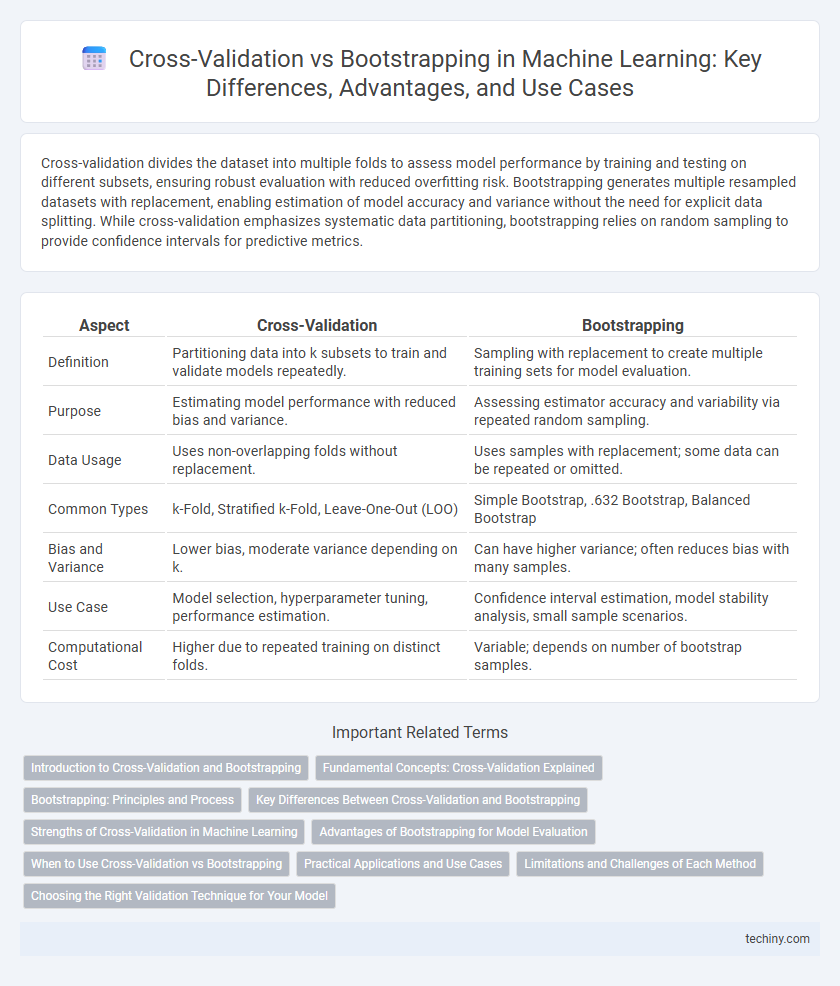
| Aspect | Cross-Validation | Bootstrapping |
|---|---|---|
| Definition | Partitioning data into k subsets to train and validate models repeatedly. | Sampling with replacement to create multiple training sets for model evaluation. |
| Purpose | Estimating model performance with reduced bias and variance. | Assessing estimator accuracy and variability via repeated random sampling. |
| Data Usage | Uses non-overlapping folds without replacement. | Uses samples with replacement; some data can be repeated or omitted. |
| Common Types | k-Fold, Stratified k-Fold, Leave-One-Out (LOO) | Simple Bootstrap, .632 Bootstrap, Balanced Bootstrap |
| Bias and Variance | Lower bias, moderate variance depending on k. | Can have higher variance; often reduces bias with many samples. |
| Use Case | Model selection, hyperparameter tuning, performance estimation. | Confidence interval estimation, model stability analysis, small sample scenarios. |
| Computational Cost | Higher due to repeated training on distinct folds. | Variable; depends on number of bootstrap samples. |
Introduction to Cross-Validation and Bootstrapping
Cross-validation and bootstrapping are essential resampling techniques in machine learning used to assess model performance and estimate prediction error. Cross-validation involves partitioning the dataset into complementary subsets to train and validate the model iteratively, commonly using k-fold methods for robust evaluation. Bootstrapping generates multiple datasets by sampling with replacement from the original data, enabling estimation of statistics and model variability without relying on strict distributional assumptions.
Fundamental Concepts: Cross-Validation Explained
Cross-validation is a statistical method used to estimate the performance of machine learning models by partitioning data into subsets, training the model on some subsets, and validating it on the remaining ones. The most common type, k-fold cross-validation, splits the dataset into k equally sized folds, iteratively using each fold as a test set while training on the others. This technique helps minimize overfitting and provides a more reliable estimate of model accuracy compared to a single train-test split.
Bootstrapping: Principles and Process
Bootstrapping is a resampling technique in machine learning that generates multiple datasets by randomly sampling with replacement from the original data, preserving the original sample size. This process allows estimation of the model's variance and bias by creating an empirical distribution of a statistic, facilitating robust performance evaluation. Unlike cross-validation, bootstrapping effectively assesses model stability, especially in small datasets, by capturing variability through repeated sampling.
Key Differences Between Cross-Validation and Bootstrapping
Cross-validation divides the dataset into distinct folds to systematically train and test the model, ensuring an unbiased estimate of performance and reducing overfitting risks. Bootstrapping generates multiple samples by random sampling with replacement, allowing estimation of the sampling distribution of a statistic and providing insights into model variability and bias. Cross-validation emphasizes model evaluation across partitions, while bootstrapping focuses on statistical inference through resampling techniques.
Strengths of Cross-Validation in Machine Learning
Cross-validation provides robust performance estimation by systematically partitioning data into training and testing sets, which reduces overfitting and bias in machine learning models. It enhances model generalization by leveraging k-fold or stratified sampling techniques to ensure representative data splits. Its ability to evaluate model stability across multiple iterations makes cross-validation a preferred method for hyperparameter tuning and model selection.
Advantages of Bootstrapping for Model Evaluation
Bootstrapping offers robust advantages for model evaluation by providing a versatile approach to estimate model accuracy and stability through repeated sampling with replacement from the original dataset. This technique enables effective assessment of model variance and bias without the need for separate validation sets, making it especially useful for small data samples. Bootstrapping also facilitates construction of confidence intervals around performance metrics, improving the reliability of model evaluations in machine learning.
When to Use Cross-Validation vs Bootstrapping
Cross-validation is best used when evaluating model performance on limited data, providing reliable estimates by partitioning the dataset into training and testing folds, which helps prevent overfitting. Bootstrapping suits scenarios requiring uncertainty estimation or small sample sizes, as it generates multiple resampled datasets to assess variability and confidence intervals in model predictions. Choosing between cross-validation and bootstrapping depends on the goal of model evaluation: error estimation favors cross-validation, while variance estimation benefits from bootstrapping.
Practical Applications and Use Cases
Cross-validation is widely used in predictive modeling to assess model performance by partitioning data into training and testing sets, ensuring robust evaluation especially in supervised learning tasks like classification and regression. Bootstrapping serves as an effective method for estimating the sampling distribution of an estimator and is commonly applied in ensemble methods such as bagging to improve model stability. Both techniques are essential in practical machine learning workflows for model validation and uncertainty estimation, with cross-validation favored for tuning hyperparameters and bootstrapping useful in variance reduction and confidence interval estimation.
Limitations and Challenges of Each Method
Cross-validation can be computationally intensive, especially with large datasets or complex models, and may produce high variance estimates if the sample size is small or folds are not properly randomized. Bootstrapping faces challenges in representing the true data distribution, as resampling with replacement can lead to biased estimates and overfitting in small datasets. Both methods struggle with dependent data structures where assumptions of independence are violated, reducing the reliability of performance metrics.
Choosing the Right Validation Technique for Your Model
Selecting the appropriate validation technique hinges on your dataset size and model complexity; cross-validation is ideal for smaller datasets as it maximizes training and testing efficiency by partitioning data into multiple folds. Bootstrapping excels in estimating model accuracy and variance through random sampling with replacement, making it suitable for assessing model stability. Leveraging cross-validation provides robust performance metrics for predictive models, while bootstrapping enables uncertainty quantification critical for statistical inference in machine learning workflows.
cross-validation vs bootstrapping Infographic
 techiny.com
techiny.com