Support Vector Machines (SVM) and Logistic Regression are powerful classification algorithms used in machine learning, each excelling in different scenarios depending on data characteristics. SVM is effective for high-dimensional spaces and works well with clear margin separation by maximizing the margin between classes, making it robust to overfitting in complex datasets. Logistic Regression offers probabilistic interpretation and performs efficiently when the relationship between features and the target variable is linear, making it suitable for simpler, well-separated data.
Table of Comparison
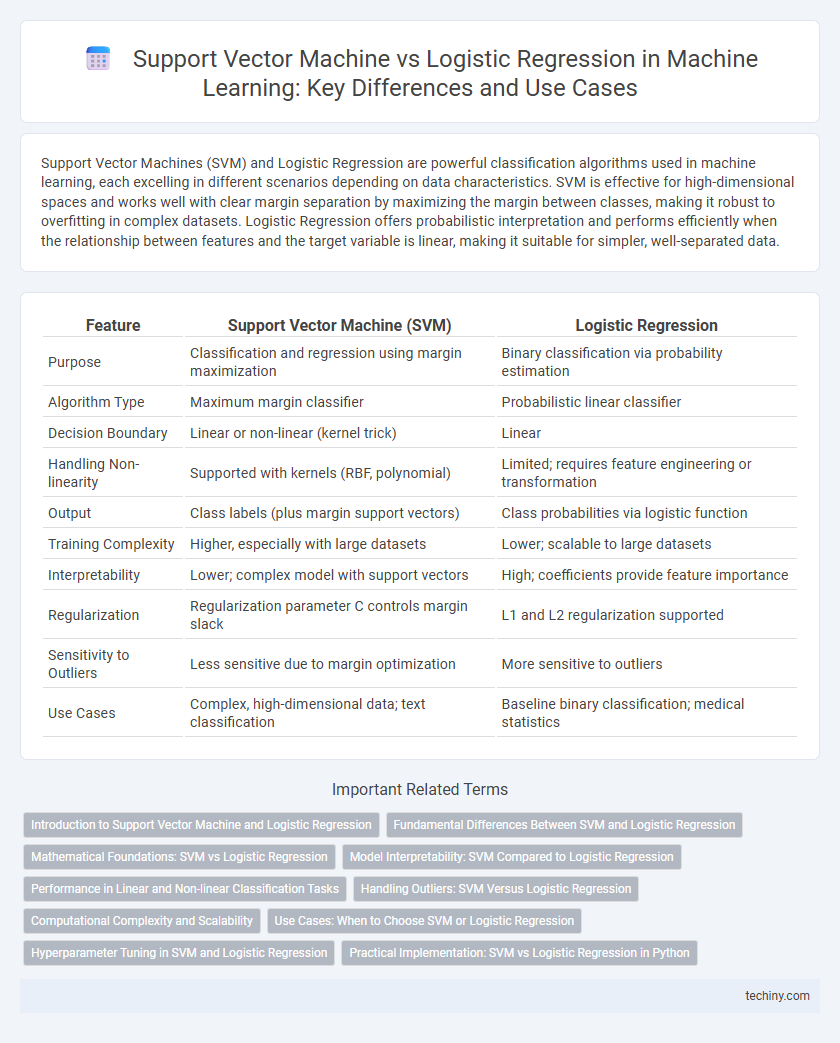
| Feature | Support Vector Machine (SVM) | Logistic Regression |
|---|---|---|
| Purpose | Classification and regression using margin maximization | Binary classification via probability estimation |
| Algorithm Type | Maximum margin classifier | Probabilistic linear classifier |
| Decision Boundary | Linear or non-linear (kernel trick) | Linear |
| Handling Non-linearity | Supported with kernels (RBF, polynomial) | Limited; requires feature engineering or transformation |
| Output | Class labels (plus margin support vectors) | Class probabilities via logistic function |
| Training Complexity | Higher, especially with large datasets | Lower; scalable to large datasets |
| Interpretability | Lower; complex model with support vectors | High; coefficients provide feature importance |
| Regularization | Regularization parameter C controls margin slack | L1 and L2 regularization supported |
| Sensitivity to Outliers | Less sensitive due to margin optimization | More sensitive to outliers |
| Use Cases | Complex, high-dimensional data; text classification | Baseline binary classification; medical statistics |
Introduction to Support Vector Machine and Logistic Regression
Support Vector Machine (SVM) is a supervised learning algorithm that constructs hyperplanes to maximize the margin between different classes, making it effective for both linear and nonlinear classification tasks through kernel functions. Logistic Regression models the probability of a binary outcome by fitting data to a logistic curve, optimizing parameters via maximum likelihood estimation to handle linearly separable data. Both algorithms serve as fundamental classifiers in machine learning, with SVM excelling in margin maximization and handling complex boundaries, while Logistic Regression offers probabilistic interpretation and simplicity.
Fundamental Differences Between SVM and Logistic Regression
Support Vector Machines (SVM) focus on finding the optimal hyperplane that maximizes the margin between classes, which enhances generalization in high-dimensional spaces. Logistic Regression estimates probabilities using a logistic function, optimizing a likelihood function to model the decision boundary. SVM handles non-linear classification efficiently through kernel tricks, whereas Logistic Regression relies on linear decision boundaries unless combined with feature transformations.
Mathematical Foundations: SVM vs Logistic Regression
Support Vector Machines (SVM) optimize the margin by solving a convex quadratic programming problem that maximizes the distance between the decision boundary and the nearest data points, relying on hinge loss as the objective function. Logistic Regression, on the other hand, models the probability of class membership using the logistic sigmoid function and optimizes parameters by minimizing the log-loss through gradient descent. SVM inherently finds a sparse solution with support vectors defining the hyperplane, while Logistic Regression yields probabilistic outputs based on all feature contributions.
Model Interpretability: SVM Compared to Logistic Regression
Support Vector Machines (SVM) tend to have lower model interpretability compared to Logistic Regression due to their reliance on kernel functions and support vectors, which obscure the direct relationship between features and predictions. Logistic Regression provides clear coefficient weights that quantify the influence of each feature, making the model inherently more interpretable. In high-dimensional datasets, SVM's complexity can hinder insights, whereas Logistic Regression's straightforward linear decision boundary facilitates better understanding and explainability.
Performance in Linear and Non-linear Classification Tasks
Support Vector Machines (SVM) often outperform Logistic Regression in non-linear classification tasks due to their ability to leverage kernel functions for complex decision boundaries. Logistic Regression excels in linear classification problems with its probabilistic output and faster training times on large datasets. In scenarios involving high-dimensional data, SVM's margin maximization generally leads to better generalization compared to Logistic Regression.
Handling Outliers: SVM Versus Logistic Regression
Support Vector Machines (SVM) handle outliers more robustly by maximizing the margin between classes and using kernel functions to separate non-linear data, effectively reducing the influence of noisy data points. Logistic regression is more sensitive to outliers because it models probabilities using a logistic function, which can be heavily affected by extreme values in the dataset. SVM's hinge loss function penalizes misclassifications but allows some margin errors, making it preferable for datasets with outliers compared to logistic regression's likelihood-based approach.
Computational Complexity and Scalability
Support Vector Machines (SVM) typically have higher computational complexity due to their quadratic optimization process, making them less scalable for very large datasets compared to Logistic Regression, which relies on convex optimization and gradient-based methods with linear time complexity. Logistic Regression scales more efficiently with increasing data size and dimensionality, benefiting from simpler model structures and faster convergence. While SVMs perform well in high-dimensional spaces, their training time and memory consumption grow significantly, impacting scalability in big data scenarios.
Use Cases: When to Choose SVM or Logistic Regression
Support Vector Machines (SVM) excel in high-dimensional spaces and complex, non-linear classification tasks, making them ideal for image recognition and text categorization where margin maximization is critical. Logistic Regression performs well with linearly separable data, offering probabilistic outputs that suit binary classification problems like credit scoring or medical diagnosis. Choosing SVM is advantageous when dealing with small to medium-sized datasets with clear margin separation, while Logistic Regression is preferable for large datasets requiring interpretability and fast training.
Hyperparameter Tuning in SVM and Logistic Regression
Support Vector Machine (SVM) hyperparameter tuning primarily involves optimizing the kernel type, regularization parameter (C), and the gamma value for non-linear kernels to enhance model generalization and margin maximization. In Logistic Regression, hyperparameter tuning focuses on selecting the regularization technique (L1, L2, or elastic net), adjusting the regularization strength (C), and optimizing the solver for efficient convergence and prevention of overfitting. Both algorithms benefit significantly from grid search or randomized search methods combined with cross-validation to identify the hyperparameters that minimize classification error and improve predictive performance.
Practical Implementation: SVM vs Logistic Regression in Python
Support Vector Machine (SVM) and Logistic Regression are both popular classifiers in Python, with SVM excelling in handling non-linear decision boundaries using kernel tricks, while Logistic Regression is preferred for its simplicity and efficiency on linearly separable data. Implementing SVM involves using libraries like scikit-learn with classes such as SVC, which offer parameters for kernel selection and regularization, whereas Logistic Regression utilizes LogisticRegression with options for penalty and solver types. Practical considerations include SVM's higher computational cost for large datasets and Logistic Regression's probabilistic output, making it suitable for interpretability and real-time applications.
support vector machine vs logistic regression Infographic
 techiny.com
techiny.com