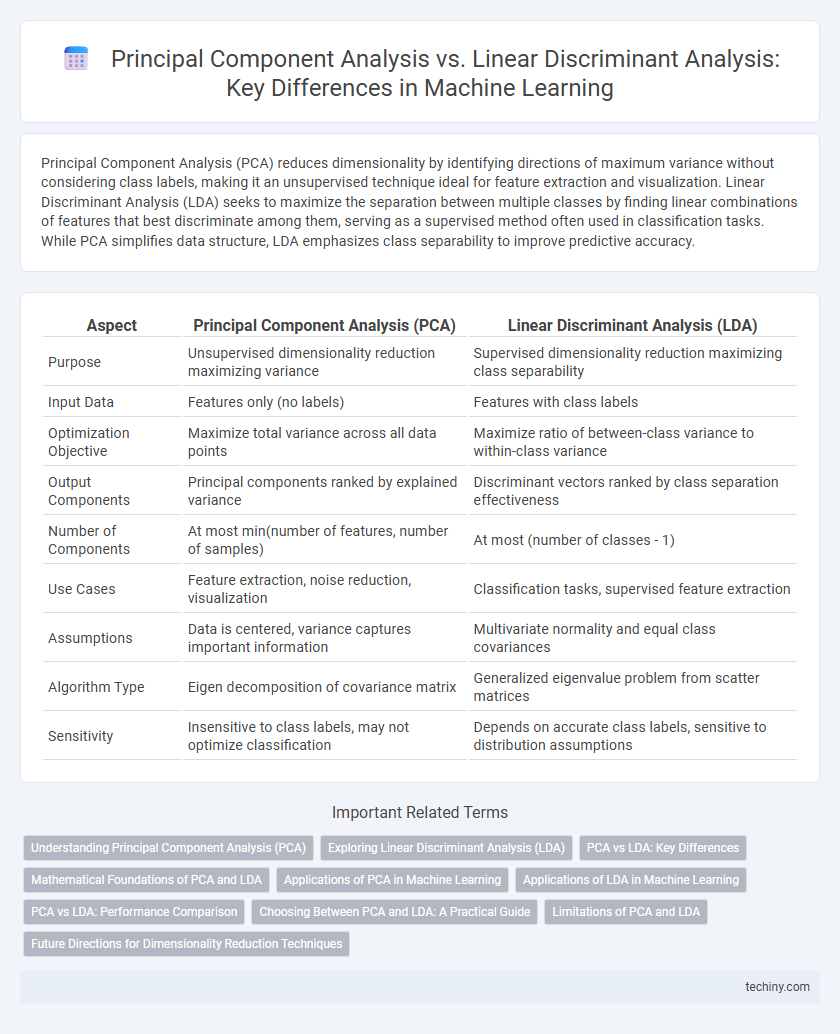
Principal Component Analysis (PCA) reduces dimensionality by identifying directions of maximum variance without considering class labels, making it an unsupervised technique ideal for feature extraction and visualization. Linear Discriminant Analysis (LDA) seeks to maximize the separation between multiple classes by finding linear combinations of features that best discriminate among them, serving as a supervised method often used in classification tasks. While PCA simplifies data structure, LDA emphasizes class separability to improve predictive accuracy.
Table of Comparison
| Aspect | Principal Component Analysis (PCA) | Linear Discriminant Analysis (LDA) |
|---|---|---|
| Purpose | Unsupervised dimensionality reduction maximizing variance | Supervised dimensionality reduction maximizing class separability |
| Input Data | Features only (no labels) | Features with class labels |
| Optimization Objective | Maximize total variance across all data points | Maximize ratio of between-class variance to within-class variance |
| Output Components | Principal components ranked by explained variance | Discriminant vectors ranked by class separation effectiveness |
| Number of Components | At most min(number of features, number of samples) | At most (number of classes - 1) |
| Use Cases | Feature extraction, noise reduction, visualization | Classification tasks, supervised feature extraction |
| Assumptions | Data is centered, variance captures important information | Multivariate normality and equal class covariances |
| Algorithm Type | Eigen decomposition of covariance matrix | Generalized eigenvalue problem from scatter matrices |
| Sensitivity | Insensitive to class labels, may not optimize classification | Depends on accurate class labels, sensitive to distribution assumptions |
Understanding Principal Component Analysis (PCA)
Principal Component Analysis (PCA) is a dimensionality reduction technique that transforms high-dimensional data into a lower-dimensional space by identifying the directions, called principal components, which maximize variance. PCA is an unsupervised method that does not consider class labels and focuses solely on capturing the most significant features of the data's covariance structure. This technique is widely used for noise reduction, visualization, and improving computational efficiency in machine learning models.
Exploring Linear Discriminant Analysis (LDA)
Linear Discriminant Analysis (LDA) is a supervised dimensionality reduction technique that maximizes class separability by projecting data onto a lower-dimensional space. Unlike Principal Component Analysis (PCA), which focuses on capturing the maximum variance regardless of class labels, LDA optimizes the ratio of between-class variance to within-class variance. This approach makes LDA particularly effective in classification tasks by enhancing class discriminability and improving model performance.
PCA vs LDA: Key Differences
Principal Component Analysis (PCA) focuses on maximizing variance by projecting data onto orthogonal components without considering class labels, making it an unsupervised dimensionality reduction technique. In contrast, Linear Discriminant Analysis (LDA) aims to maximize class separability by finding linear combinations of features that best discriminate between predefined classes, functioning as a supervised method. PCA is typically used for feature extraction when the primary goal is data compression, while LDA is preferred for classification tasks where maximizing between-class variance relative to within-class variance is crucial.
Mathematical Foundations of PCA and LDA
Principal Component Analysis (PCA) relies on eigenvalue decomposition of the covariance matrix to identify directions of maximum variance in the data, projecting it onto orthogonal components without using class labels. Linear Discriminant Analysis (LDA) maximizes the ratio of between-class scatter to within-class scatter matrices by solving a generalized eigenvalue problem, optimizing class separability. PCA focuses on capturing overall data variance through principal components, while LDA emphasizes discriminative directions based on class separation via linear combinations of features.
Applications of PCA in Machine Learning
Principal Component Analysis (PCA) is widely applied in machine learning for dimensionality reduction, feature extraction, and data visualization by identifying the directions of maximum variance in high-dimensional datasets. PCA enhances model performance by reducing overfitting and computational complexity while preserving essential information. Common applications include preprocessing steps in image recognition, gene expression analysis, and customer segmentation, where it helps to improve the efficiency and interpretability of predictive models.
Applications of LDA in Machine Learning
Linear Discriminant Analysis (LDA) is widely used in machine learning for dimensionality reduction and classification tasks, particularly in scenarios with labeled data such as facial recognition, speech recognition, and medical diagnosis. LDA maximizes the separability between multiple classes by projecting features onto a lower-dimensional space, improving class discrimination compared to unsupervised methods like Principal Component Analysis (PCA). Its effectiveness in enhancing classifier performance makes LDA especially valuable for pattern recognition and supervised learning problems.
PCA vs LDA: Performance Comparison
Principal Component Analysis (PCA) focuses on maximizing variance to identify principal components, making it ideal for unsupervised dimensionality reduction, while Linear Discriminant Analysis (LDA) maximizes class separability by optimizing the ratio of between-class variance to within-class variance, benefiting supervised classification tasks. Performance comparisons reveal PCA is more effective for feature extraction when class labels are unavailable, whereas LDA generally outperforms PCA in classification accuracy due to its use of label information. In scenarios with limited sample sizes or overlapping classes, LDA may suffer from singularity issues, whereas PCA remains robust, highlighting the trade-offs between variance preservation and class discrimination.
Choosing Between PCA and LDA: A Practical Guide
Choosing between Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA) depends on the goal of dimensionality reduction versus classification. PCA is unsupervised, focusing on maximizing variance and capturing the most informative features without considering class labels, making it ideal for exploratory data analysis and noise reduction. LDA, a supervised method, seeks to maximize class separability by considering class labels, which enhances performance in classification tasks where labeled data is available.
Limitations of PCA and LDA
Principal Component Analysis (PCA) struggles with capturing class separability since it focuses on maximizing variance without considering class labels, which can lead to suboptimal feature discrimination in classification tasks. Linear Discriminant Analysis (LDA) assumes normally distributed classes with equal covariance matrices, limiting its effectiveness when these assumptions are violated or in cases of small sample size relative to feature dimension. Both PCA and LDA can suffer from the curse of dimensionality, but LDA's reliance on labeled data restricts its applicability in unsupervised or weakly supervised settings.
Future Directions for Dimensionality Reduction Techniques
Future directions in dimensionality reduction techniques emphasize integrating Principal Component Analysis (PCA) with nonlinear methods to enhance data representation in complex feature spaces. Advances in Linear Discriminant Analysis (LDA) focus on robust algorithms that can handle imbalanced and high-dimensional datasets more effectively. Emerging hybrid models are designed to leverage the strengths of both PCA and LDA, optimizing feature extraction for improved machine learning performance.
Principal Component Analysis vs Linear Discriminant Analysis Infographic
 techiny.com
techiny.com